题目内容
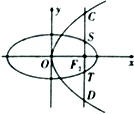如图，椭圆E：| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| |CD| |
| |ST| |
| 3 |
（Ⅰ）求椭圆E的方程；
（Ⅱ）若过点M（3，0）的直线l与椭圆E交于两点A、B，设P为椭圆上一点，且满足
| OA |
| OB |
| OP |
考点：直线与圆锥曲线的关系,椭圆的标准方程
专题：综合题,圆锥曲线的定义、性质与方程
分析：（1）由焦点F2（
，0），故可设椭圆的方程为
+
=1，求出C，D的坐标，由抛物线与椭圆的对称性，可得S（
，
），代入椭圆方程，即可求椭圆E的方程；
（Ⅱ）分类讨论，设出直线的方程，代入椭圆方程，利用韦达定理，结合
+
=t
，求出P的坐标，代入椭圆方程，求出实数t的取值范围．
| 3 |
| x2 |
| b2+3 |
| y2 |
| b2 |
| 3 |
| 1 |
| 2 |
（Ⅱ）分类讨论，设出直线的方程，代入椭圆方程，利用韦达定理，结合
| OA |
| OB |
| OP |
解答：
解：（Ⅰ）由抛物线方程，得焦点F2（
，0），故可设椭圆的方程为
+
=1，
解方程组
解得C（
，2
），D（
，-2
），
由抛物线与椭圆的对称性，可得：
=
=4
，所以|F2S|=
，所以S（
，
）．
因此
+
=1，解得b=1，故而a=2，
所以椭圆E的方程为
+y2=1．
（Ⅱ）由题意知直线l的斜率存在，设其为k．
①当k=0时，所以t=0；
②当k≠0时，则直线l的方程为y=k（x-3），
代入椭圆方程，消去y并整理得：（1+4k2）x2-24k2x+36k2-4=0，
由△＞0，得0＜k2＜
，
设A（x1，y1），B（x2，y2），P（x0，y0），则x1+x2=
，x1x2=
．
因为
+
=t
，所以（x1+x2，y1+y2）=t（x0，y0），
所以x0=
（x1+x2）=
，y0=
．
因为点P在椭圆上，所以[
]2+[
]2=4，
解得t2=9-
，
由于0＜k2＜
，故而0＜t2＜4，所以t∈（-2，0）∪（0，2），
综合①②可知，t∈（-2，2）．
| 3 |
| x2 |
| b2+3 |
| y2 |
| b2 |
解方程组
|
| 3 |
| 3 |
| 3 |
| 3 |
由抛物线与椭圆的对称性，可得：
| |F2C| |
| |F2S| |
| |CD| |
| |ST| |
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
因此
| 3 |
| b2+3 |
| ||
| b2 |
所以椭圆E的方程为
| x2 |
| 4 |
（Ⅱ）由题意知直线l的斜率存在，设其为k．
①当k=0时，所以t=0；
②当k≠0时，则直线l的方程为y=k（x-3），
代入椭圆方程，消去y并整理得：（1+4k2）x2-24k2x+36k2-4=0，
由△＞0，得0＜k2＜
| 1 |
| 5 |
设A（x1，y1），B（x2，y2），P（x0，y0），则x1+x2=
| 24k2 |
| 1+4k2 |
| 36k2-4 |
| 1+4k2 |
因为
| OA |
| OB |
| OP |
所以x0=
| 1 |
| t |
| 24k2 |
| t(1+4k2) |
| -6k |
| t(1+4k2) |
因为点P在椭圆上，所以[
| 24k2 |
| t(1+4k2) |
| -6k |
| t(1+4k2) |
解得t2=9-
| 9 |
| 1+4k2 |
由于0＜k2＜
| 1 |
| 5 |
综合①②可知，t∈（-2，2）．
点评：本题重点考查圆锥曲线的方程，考查直线与圆锥曲线的位置关系，解题的关键是利用待定系数法求圆锥曲线的方程．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
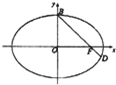如图，已知F是椭圆C的一个焦点，B是短轴的一个端点，线段BF的延长线交椭圆C于点D，且