Question

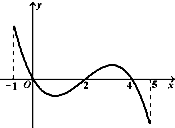已知函数f（x）的定义域为[-1，5]，部分对应值如下表，f（x）的导函数y=f′（x）的图象如图所示．下列关于f（x）的命题：

x	-1	0	4	5
f（x）	1	2	2	1

①函数f（x）的极大值点为0，4；
②函数f（x）在[0，2]上是减函数；
③如果当x∈[-1，t]时，f（x）的最大值是2，那么t的最大值为4；
④当1＜a＜2时，函数y=f（x）-a有4个零点．
其中正确命题的个数有

 

 个．

Answer 1

考点：命题的真假判断与应用

专题：函数的性质及应用,导数的综合应用

分析：本题考查利导函数判断函数单调性和极值的问题，先利用导函数图象求函数极值和单调性，然后判断正误．

解答： 解：①导函数图象在x=0和4处导数为0，且导数符号由正到负，函数f（x）先增后减，函数f（x）的极大值点为0，4，正确；
②导函数图象在x∈[0，4]处恒在x轴下侧，f′（x）≤0，函数f（x）在[0，2]上是减函数，正确；
③如果当x∈[-1，t]时，f（x）的最大值是2，那么t的最大值为5，而不是4，错误；
④由导函数图象得，函数在x=0，2，4处取得极值2，f（2），2，而当x取端点值f（-1）=f（5）=1，
则当f（2）＜1时，函数的值域为[f（2），2]，结合函数性质，当1＜a＜2时，函数y=f（x）-a有4个零点；
则当f（2）≥1时，函数的值域为[1，2]，结合函数性质，当1＜a＜2时，函数y=f（x）-a有2个零点；
综上当1＜a＜2时，函数y=f（x）-a有2或4个零点，④错误．
故答案为：2．

点评：难点是④y=f（x）-a中零点个数转化为方程f（x）=a的解的个数，可数形结合，画图求解．