题目内容
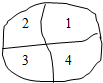 用红、黄、蓝、白、黑五种颜色涂在如图所示的四个区域内,每个区域涂一种颜色,相邻两个区域涂不同的颜色,如果颜色可以反复使用,则不同的涂色方法有
用红、黄、蓝、白、黑五种颜色涂在如图所示的四个区域内,每个区域涂一种颜色,相邻两个区域涂不同的颜色,如果颜色可以反复使用,则不同的涂色方法有考点:排列、组合的实际应用
专题:计算题,概率与统计
分析:根据题意,分2步进行分析:先涂1号区域,易得其有5种涂法,再分类讨论其他区域:①若2、4号区域涂不同的颜色,②若2、4号区域涂相同的颜色,分别求出2、3、4号区域的涂色方案数目再相加可得其他区域涂色方案数目;由分步计数原理计算可得答案.
解答:
解:对于1号区域,有5种颜色可选,即有5种涂法,
分类讨论其他区域:①若2、4号区域涂不同的颜色,则有A42=12种涂法,3号区域有3种涂法,此时2、3、4号区域有12×3=36种涂法;
②若2、4号区域涂相同的颜色,则有4种涂法,3号区域有4种涂法,此时2、3、4号区域有有4×4=16种涂法;
则共有5×(36+16)=5×52=260种;
故答案为260.
分类讨论其他区域:①若2、4号区域涂不同的颜色,则有A42=12种涂法,3号区域有3种涂法,此时2、3、4号区域有12×3=36种涂法;
②若2、4号区域涂相同的颜色,则有4种涂法,3号区域有4种涂法,此时2、3、4号区域有有4×4=16种涂法;
则共有5×(36+16)=5×52=260种;
故答案为260.
点评:本题考查分类计数原理与分步计数原理的运用,注意本题中2、4号区域的颜色相同与否对3号区域有影响,需要分类讨论.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
已知函数f(x+1)=x2+2x-1,x∈[1,2],则f(x)是( )
| A、[1,2]上的增函数 |
| B、[1,2]上的减函数 |
| C、[2,3]上的增函数 |
| D、[2,3]上的减函数 |
下列各列数都是依照一定的规律排列,在括号里填上适当的数2,3,5,8,12,( )
| A、20 | B、19 | C、18 | D、17 |
已知复数z满足|(1-i)z=i2014(其中i为虚数单位),则
的虚部为( )
. |
| z |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
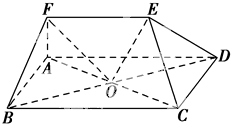 在多面体ABCDEF中,点O是矩形ABCD的对角线的交点,三角形CDE是等边三角形,棱EF∥BC且EF=
在多面体ABCDEF中,点O是矩形ABCD的对角线的交点,三角形CDE是等边三角形,棱EF∥BC且EF=