题目内容
已知函数f(x+1)=x2+2x-1,x∈[1,2],则f(x)是( )
| A、[1,2]上的增函数 |
| B、[1,2]上的减函数 |
| C、[2,3]上的增函数 |
| D、[2,3]上的减函数 |
考点:函数解析式的求解及常用方法,函数单调性的判断与证明
专题:计算题,函数的性质及应用
分析:由x∈[1,2],则x+1∈[2,3],即f(x)的定义域为[2,3],化简f(x)=x2-2,则在[2,3]上是增函数.
解答:
解:∵x∈[1,2],∴x+1∈[2,3],
故f(x)的定义域为[2,3],
又∵f(x+1)=x2+2x-1=(x+1)2-2,
∴f(x)=x2-2,
则其在[2,3]上是增函数,
故选C.
故f(x)的定义域为[2,3],
又∵f(x+1)=x2+2x-1=(x+1)2-2,
∴f(x)=x2-2,
则其在[2,3]上是增函数,
故选C.
点评:本题考查了函数的定义域的求法及函数解析式的求法,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
过点P(4,2)作圆x2+y2=4的两条切线,切点分别为A,B,O为原点,则△OAB的外接圆方程是( )
| A、(x-2)2+(y-1)2=5 |
| B、(x-4)2+(y-2)2=20 |
| C、(x+2)2+(y+1)2=5 |
| D、(x+4)2+(y+2)2=20 |
若
•
+
=0,则△ABC为( )
| AB |
| BC |
| AB2 |
| A、直角三角形 |
| B、钝角三角形 |
| C、锐角三角形 |
| D、等腰三角形 |
在复平面内,复数3-4i,i(2+i)对应的点分别为A、B,则线段AB的中点C对应的复数为( )
| A、-2+2i | B、2-2i |
| C、-1+i | D、1-i |
已知集合M={(x,y)|y2=x+1},下列关系式中正确的是( )
| A、-1,0∈M |
| B、{-1,0}∈M |
| C、(-1,0)∈M |
| D、(-1,0)∉M |
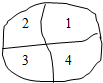 用红、黄、蓝、白、黑五种颜色涂在如图所示的四个区域内,每个区域涂一种颜色,相邻两个区域涂不同的颜色,如果颜色可以反复使用,则不同的涂色方法有
用红、黄、蓝、白、黑五种颜色涂在如图所示的四个区域内,每个区域涂一种颜色,相邻两个区域涂不同的颜色,如果颜色可以反复使用,则不同的涂色方法有