题目内容
设直线l的方程为(a+1)x+y+2-a=0(a∈R),若l在两坐标轴上的截距相等,求l的方程.
考点:直线的一般式方程
专题:直线与圆
分析:分别令x,y等于0,代入已知方程可得两截距,由题意可得a的方程,解a值可得答案.
解答:
解:令x=0可得y=a-2,即直线在y轴的截距为a-2,
∵l在两坐标轴上的截距相等,∴a+1≠0
∴令y=0可得x=
,
∴a-2=
,解得a=2或a=0
∴l的方程为:3x+y=0或x+y+2=0
∵l在两坐标轴上的截距相等,∴a+1≠0
∴令y=0可得x=
| a-2 |
| a+1 |
∴a-2=
| a-2 |
| a+1 |
∴l的方程为:3x+y=0或x+y+2=0
点评:本题考查直线的一般式方程,涉及直线的截距,属基础题.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
已知cosα-sinα=
,则sin2α的值为( )
| 1 |
| 2 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
已知集合M={(x,y)|y2=x+1},下列关系式中正确的是( )
| A、-1,0∈M |
| B、{-1,0}∈M |
| C、(-1,0)∈M |
| D、(-1,0)∉M |
与y=x为同一个函数的是( )
A、y=
| |||
B、y=
| |||
C、
| |||
D、y=(
|
i为虚数单位,(1-i)2=( )
| A、-2 i |
| B、2 i |
| C、1-2 i |
| D、2-2 i |
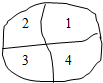 用红、黄、蓝、白、黑五种颜色涂在如图所示的四个区域内,每个区域涂一种颜色,相邻两个区域涂不同的颜色,如果颜色可以反复使用,则不同的涂色方法有
用红、黄、蓝、白、黑五种颜色涂在如图所示的四个区域内,每个区域涂一种颜色,相邻两个区域涂不同的颜色,如果颜色可以反复使用,则不同的涂色方法有
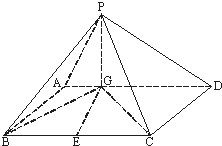 如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上且AG=
如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上且AG=