题目内容
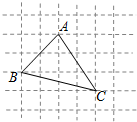
△ABC的顶点A,B,C在正方形网格中的位置如图所示.则cos(B+C)= .

考点:两角和与差的余弦函数
专题:三角函数的求值
分析:△ABC中,由余弦定理求得cosA的值,再根据cos(B+C)=-cosA可得结果.
解答:
解:由所给的图形可得AB=2
,BC=
,AC=
=
,
△ABC中,由余弦定理可得 cosA=
=
=
,
∴cos(B+C)=-cosA=-
故答案为:-
.
| 2 |
| 17 |
| 4+9 |
| 13 |
△ABC中,由余弦定理可得 cosA=
| AB2+AC2-BC2 |
| 2AB•AC |
| 8+13-17 | ||||
4
|
| ||
| 26 |
∴cos(B+C)=-cosA=-
| ||
| 26 |
故答案为:-
| ||
| 26 |
点评:本题主要考查诱导公式、余弦定理的应用,属于中档题.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
命题“?数列{an},{bn}既是等差数列,又是等比数列”( )
| A、是特称命题并且是假命题 |
| B、是全称命题并且是假命题 |
| C、是特称命题并且是真命题 |
| D、是全称命题并且是真命题 |
阅读如图的程序框图,运行相应的程序,则输出S的值为( )


| A、2013×1006 |
| B、2013×1007 |
| C、2015×1007 |
| D、2015×1008 |
若复数z满足(z-3)(2-i)=5(i为虚数单位),则在复平面内z对应的点在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
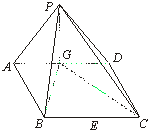 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠DAB=60°.侧面PAD为正三角形,其所在的平面垂直于底面ABCD,G为AD边的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠DAB=60°.侧面PAD为正三角形,其所在的平面垂直于底面ABCD,G为AD边的中点.