题目内容
已知函数f(x)=
sin2x+2cos2x+m在区间[0,
]上的最大值为3,则
(Ⅰ)m= ;
(Ⅱ)对任意a∈R,f(x)在[a,a+20π]上的零点个数为 .
| 3 |
| π |
| 2 |
(Ⅰ)m=
(Ⅱ)对任意a∈R,f(x)在[a,a+20π]上的零点个数为
考点:三角函数中的恒等变换应用
专题:解三角形
分析:(Ⅰ)利用二倍角公式和两角和公式对函数解析式化简整理,利用函数的最大值,求得m的值.
(Ⅱ)根据已知推断区间的长度为20π,求得函数的最小正周期,推断出在此区间共有多少个周期,利用每个周期内零点的个数推断出共计的零点个数.
(Ⅱ)根据已知推断区间的长度为20π,求得函数的最小正周期,推断出在此区间共有多少个周期,利用每个周期内零点的个数推断出共计的零点个数.
解答:
解:(Ⅰ)f(x)=
sin2x+2cos2x+m=
sin2x+cos2x+1+m=2(
sin2x+
cos2x)+1+m=2sin(2x+
)+1+m,
∵x∈[0,
],
∴2x+
∈[
,
]
∵sin(2x+
)最大值为1,
∴f(x)max=3+m=3,此时m=0.
(Ⅱ)由(Ⅰ)知f(x)=2sin(2x+
)+1,
∴T=
=π,
∴对于区间[a,a+20π]的长度为20π+a-a=20π,
∴在此区间上,函数f(x)可以有20个周期,
当a=-
+kπ(k∈Z)时,在第一个周期内恰有3个零点,以后每个周期均由2个零点,则此时零点个数为:20×2+1=41.
当a≠-
+kπ(k∈Z)时,在每个周期内有2个零点,则此时零点个数为:20×2=40.
综合得零点的个数为40或41个,
故答案为:40或41.
| 3 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
∵x∈[0,
| π |
| 2 |
∴2x+
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
∵sin(2x+
| π |
| 6 |
∴f(x)max=3+m=3,此时m=0.
(Ⅱ)由(Ⅰ)知f(x)=2sin(2x+
| π |
| 6 |
∴T=
| 2π |
| 2 |
∴对于区间[a,a+20π]的长度为20π+a-a=20π,
∴在此区间上,函数f(x)可以有20个周期,
当a=-
| π |
| 12 |
当a≠-
| π |
| 12 |
综合得零点的个数为40或41个,
故答案为:40或41.
点评:本题主要考查了三角形恒等变换的应用,三角函数图象与性质.此题要特别考虑到a=-
+kπ这一特殊情况,防止漏解.
| π |
| 12 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
命题“?数列{an},{bn}既是等差数列,又是等比数列”( )
| A、是特称命题并且是假命题 |
| B、是全称命题并且是假命题 |
| C、是特称命题并且是真命题 |
| D、是全称命题并且是真命题 |
已知a∈{2,3},b∈{1,2,3},执行如图所示程序框图,则输出的结果共有( )


| A、3种 | B、4种 | C、5种 | D、6种 |
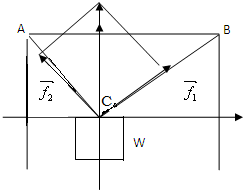 物体W的质量为50千克,用绳子将物体W悬挂在两面墙之间,已知两面墙之间的距离AB=10米(AB为水平线),AC=6米,BC=8米,求AC,BC上所受的力的大小.
物体W的质量为50千克,用绳子将物体W悬挂在两面墙之间,已知两面墙之间的距离AB=10米(AB为水平线),AC=6米,BC=8米,求AC,BC上所受的力的大小.