题目内容
已知G是△ABC的重心，直线EF过点G且与边AB、C分别交于点E、F，
=α
，
=β
，则
+
的值为 ．
| AE |
| AB |
| AF |
| AC |
| 1 |
| α |
| 1 |
| β |
考点：向量加减混合运算及其几何意义
专题：平面向量及应用
分析：利用向量共线定理可得：存在实数λ三点
=λ
+(1-λ)
，由于
=α
，
=β
，可得
=λα
+(1-λ)β
．再利用G是△ABC的重心，可得
=
+
．再利用向量基本定理即可得出．
| AG |
| AE |
| AF |
| AE |
| AB |
| AF |
| AC |
| AG |
| AB |
| AC |
| AG |
| 1 |
| 3 |
| AB |
| 1 |
| 3 |
| AC |
解答：
解：如图所示，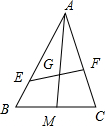
∵三点E，G，F共线，
∴存在实数λ三点
=λ
+(1-λ)
，
∵
=α
，
=β
，
∴
=λα
+(1-λ)β
．
∵G是△ABC的重心，
∴
=
，
=
(
+
)，
∴
=
+
．
∴λα=
，(1-λ)β=
，
∴
+
=3λ+3（1-λ）=3．
故答案为：3．
∵三点E，G，F共线，
∴存在实数λ三点
| AG |
| AE |
| AF |
∵
| AE |
| AB |
| AF |
| AC |
∴
| AG |
| AB |
| AC |
∵G是△ABC的重心，
∴
| AG |
| 2 |
| 3 |
| AM |
| AM |
| 1 |
| 2 |
| AB |
| AC |
∴
| AG |
| 1 |
| 3 |
| AB |
| 1 |
| 3 |
| AC |
∴λα=
| 1 |
| 3 |
| 1 |
| 3 |
∴
| 1 |
| α |
| 1 |
| β |
故答案为：3．
点评：本题考查了向量关系定理、向量基本定理、三角形重心的性质等基础知识与基本技能方法，考查了推理能力和计算能力，属于难题．
练习册系列答案
相关题目
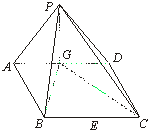如图，在四棱锥P-ABCD中，底面ABCD是边长为2的菱形，且∠DAB=60°．侧面PAD为正三角形，其所在的平面垂直于底面ABCD，G为AD边的中点．