Question

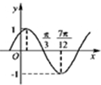
函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|＜π）的图象如图所示，则其中ω，φ分别为（　　）

• A、ω=-2，φ=

  π

  3

• B、ω=2，φ=

  π

  3

• C、ω=2，φ=-

  2π

  3

• D、ω=-2，φ=-

  π

  3

Answer 1

考点：函数y=Asin（ωx+φ）的图象变换

专题：三角函数的图像与性质

分析：利用f（x）=Asin（ωx+φ）的图象，可得A=1，

1

4

T=

π

4

，从而可求得ω；再由其图象过（

π

3

，0），|φ|＜π，可求得φ，从而可得答案．

解答： 解：由图知A=1，

1

4

T=

7π

12

-

π

3

=

π

4

，ω＞0，
∴T=

2π

ω

=π，
解得：ω=2；
又该函数的图象过（

π

3

，0），|
∴2×

π

3

+φ=2kπ+π（k∈Z），
∴φ=2kπ+

π

3

（k∈Z），又|φ|＜π，
∴φ=

π

3

；
综上所述，ω=2，φ=

π

3

．
故选：B．

点评：本题考查函数y=Asin（ωx+φ）的解析式的确定，着重考查正弦函数的图象与性质，求得φ是难点，属于中档题．