题目内容
复数z=
,
是z的共轭复数,则z+
=( )
| 2i |
| 1+i |
. |
| z |
. |
| z |
| A、4 | B、-4 | C、2 | D、-2 |
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:利用两个复数代数形式的乘除法法则化简复数z为1+i,可得
,从而求得z+
.
. |
| z |
. |
| z |
解答:
解:∵复数z=
=
=
=1+i,
∴
=1-i,∴z+
=2,
故选:C.
| 2i |
| 1+i |
| 2i•(1-i) |
| (1+i)(1-i) |
| 2+2i |
| 2 |
∴
. |
| z |
. |
| z |
故选:C.
点评:本题主要考查复数的基本概念,两个复数代数形式的乘除法法则,虚数单位i的幂运算性质,属于基础题.

练习册系列答案
相关题目
设x、y满足约束条件
,若z=x2+y2,则z的最小值为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
i是虚数单位.已知复数z=
,则复数Z对应点落在( )
| i-2 |
| 1-i |
| A、第四象限 | B、第三象限 |
| C、第二象限 | D、第一象限 |
 某高中男子体育小组的50米跑成绩(单位:s)为6.4,6.5,7.0,6.8,7.1,7.3,6.9,7.4,7.5,如图是从这些成绩中搜索处小于6.8s的成绩的一个程序框图,则图中①②分别填上( )
某高中男子体育小组的50米跑成绩(单位:s)为6.4,6.5,7.0,6.8,7.1,7.3,6.9,7.4,7.5,如图是从这些成绩中搜索处小于6.8s的成绩的一个程序框图,则图中①②分别填上( )| A、r≥6.8,n>9? |
| B、r<6.8,n>9? |
| C、r≥6.8,n≤9? |
| D、r<6.8,n≤9? |
函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<π)的图象如图所示,则其中ω,φ分别为( )
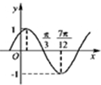

A、ω=-2,φ=
| ||
B、ω=2,φ=
| ||
C、ω=2,φ=-
| ||
D、ω=-2,φ=-
|
 如图,有16个格点,每个格点小正方形的面积为1,给图中间的小正方形内任意投点P,则点P落在图中阴影部分的概率是( )
如图,有16个格点,每个格点小正方形的面积为1,给图中间的小正方形内任意投点P,则点P落在图中阴影部分的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
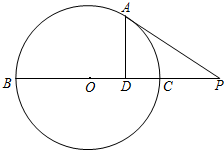 如图所示,PA与圆O相切于A,直线PO交圆O于B,C两点,AD⊥BC,垂足为D,且D是OC的中点,若PA=6,则PC=
如图所示,PA与圆O相切于A,直线PO交圆O于B,C两点,AD⊥BC,垂足为D,且D是OC的中点,若PA=6,则PC=