题目内容
函数f（x）=2|sinx|是（ ）
| A、最小正周期为2π的奇函数 |
| B、最小正周期为2π的偶函数 |
| C、最小正周期为π的奇函数 |
| D、最小正周期为π的偶函数 |
考点：三角函数的周期性及其求法,函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：利用函数的奇偶性与周期性的概念，通过判断、排除即可得到答案．
解答：
解：∵f（-x）=2|sin（-x）|=2|-sinx|=2|sinx|=f（x），
∴f（x）=2|sinx|是偶函数，可排除A，C；
又f（x+π）=2|sin（x+π）|=2|-sinx|=2|sinx|=f（x），
∴函数f（x）=2|sinx|是以π为最小正周期的函数，可排除B；
故选：C．
∴f（x）=2|sinx|是偶函数，可排除A，C；
又f（x+π）=2|sin（x+π）|=2|-sinx|=2|sinx|=f（x），
∴函数f（x）=2|sinx|是以π为最小正周期的函数，可排除B；
故选：C．
点评：本题考查三角函数的奇偶性与周期性及其求法，考查分析运算能力，属于中档题．
练习册系列答案
长江作业本同步练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
相关题目
在一次抛硬币实验中，甲、乙两人各抛一枚硬币一次，设命题p是“甲抛的硬币正面向上”，q是“乙抛的硬币正面向上”，则命题“至少有一人抛的硬币是正面向下”可表示为（ ）
| A、（￢p）∨（￢q） |
| B、p∧（￢q） |
| C、（￢p）∧（￢q） |
| D、p∨q |
i是虚数单位．已知复数z=
，则复数Z对应点落在（ ）
| i-2 |
| 1-i |
| A、第四象限 | B、第三象限 |
| C、第二象限 | D、第一象限 |
函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|＜π）的图象如图所示，则其中ω，φ分别为（ ）
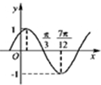
A、ω=-2，φ=
| ||
B、ω=2，φ=
| ||
C、ω=2，φ=-
| ||
D、ω=-2，φ=-
|
已知集合A={-1，
}，B={x|mx-1=0}，若A∩B=B，则所有实数m组成的集合是（ ）
| 1 |
| 2 |
| A、{0，-1，2} | ||
B、{-
| ||
| C、{-1，2} | ||
D、{-1，0，
|
如图，有16个格点，每个格点小正方形的面积为1，给图中间的小正方形内任意投点P，则点P落在图中阴影部分的概率是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|