题目内容
已知随机变量Z服从正态分布N（0，σ2），若P（Z＞1）=0.023，则P（-1≤Z≤1）=（ ）
| A、0.625 |
| B、0.954 |
| C、0.477 |
| D、0.977 |
考点：正态分布曲线的特点及曲线所表示的意义
专题：计算题,概率与统计
分析：根据随机变量ξ服从正态分布N（0，σ2），得到正态密度曲线关于y轴对称，根据P（Z＞1）=0.023，得到对称区间上的概率，从而可求P（-1≤Z≤1）．
解答：
解：由随机变量ξ服从正态分布N（0，σ2）可知正态密度曲线关于y轴对称，
∵P（Z＞1）=0.023，
∴P（-1≤Z≤1）=1-2×0.023=0.954．
故选：B．
∵P（Z＞1）=0.023，
∴P（-1≤Z≤1）=1-2×0.023=0.954．
故选：B．
点评：本题考查正态分布曲线的特点及曲线所表示的意义，考查正态曲线的对称性，考查对称区间的概率相等，本题是一个基础题．
练习册系列答案
相关题目
若圆（x-3）2+（y+5）2=r2上的点到直线4x-3y-2=0的最近距离等于1，则半径r的值为（ ）
| A、4 | B、5 | C、6 | D、9 |
某高中男子体育小组的50米跑成绩（单位：s）为6.4，6.5，7.0，6.8，7.1，7.3，6.9，7.4，7.5，如图是从这些成绩中搜索处小于6.8s的成绩的一个程序框图，则图中①②分别填上（ ）| A、r≥6.8，n＞9？ |
| B、r＜6.8，n＞9？ |
| C、r≥6.8，n≤9？ |
| D、r＜6.8，n≤9？ |
函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|＜π）的图象如图所示，则其中ω，φ分别为（ ）
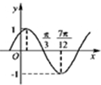
A、ω=-2，φ=
| ||
B、ω=2，φ=
| ||
C、ω=2，φ=-
| ||
D、ω=-2，φ=-
|
与30°角终边相同的角的集合是（ ）
| A、{θ|θ=30°+k•360°，k∈Z} |
| B、{θ|θ=30°+2k•360°，k∈Z} |
| C、{θ|θ=30°+k•180°，k∈Z} |
| D、{θ|θ=30°+k•90°，k∈Z} |
如图，有16个格点，每个格点小正方形的面积为1，给图中间的小正方形内任意投点P，则点P落在图中阴影部分的概率是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|