题目内容
设[x]表示不大于x的最大整数,则函数y=[lgx-1]-2lgx+1的零点之积为( )
| A、1 | ||||
B、
| ||||
C、
| ||||
D、-
|
考点:函数零点的判定定理
专题:函数的性质及应用
分析:先将函数化简,再讨论x的取值范围,求出两个零点相乘即可.
解答:
解:∵y=[lgx]-2lgx,
①x=1是零点,
②x>1时,y<0,
③0<x≤
时,y>0,
∴只需讨论
<x<1的情况,
∴[lgx]-2lgx=-1-2lgx=0,
解得:x=10-
=
,
∴零点之积为:1×
=
,
故选:B.
①x=1是零点,
②x>1时,y<0,
③0<x≤
| 1 |
| 10 |
∴只需讨论
| 1 |
| 10 |
∴[lgx]-2lgx=-1-2lgx=0,
解得:x=10-
| 1 |
| 2 |
| ||
| 10 |
∴零点之积为:1×
| ||
| 10 |
| ||
| 10 |
故选:B.
点评:本题考察了函数的零点问题,渗透了分类讨论思想,是一道基础题.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
阅读如图的程序框图,则输出的S等于( )


| A、-51 | B、50 |
| C、-50 | D、51 |
i是虚数单位.已知复数z=
,则复数Z对应点落在( )
| i-2 |
| 1-i |
| A、第四象限 | B、第三象限 |
| C、第二象限 | D、第一象限 |
某几何体的三视图如图所示,则该几何体的体积为( )


| A、54+54π |
| B、54+27π |
| C、27+27π |
| D、27+54π |
函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<π)的图象如图所示,则其中ω,φ分别为( )
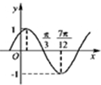

A、ω=-2,φ=
| ||
B、ω=2,φ=
| ||
C、ω=2,φ=-
| ||
D、ω=-2,φ=-
|
已知集合A={-1,
},B={x|mx-1=0},若A∩B=B,则所有实数m组成的集合是( )
| 1 |
| 2 |
| A、{0,-1,2} | ||
B、{-
| ||
| C、{-1,2} | ||
D、{-1,0,
|
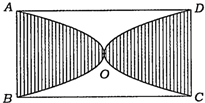 如图,矩形ABCD的面积为3,以矩形的中心O为顶点作两条抛物线,分别过点A、B和点C、D,若在矩形ABCD中随机撒入300颗豆子,则落在阴影部分内的豆子大约是
如图,矩形ABCD的面积为3,以矩形的中心O为顶点作两条抛物线,分别过点A、B和点C、D,若在矩形ABCD中随机撒入300颗豆子,则落在阴影部分内的豆子大约是