题目内容
在区间[-3，3]上任取两数x，y，使x2-y-1＜0成立的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：几何概型
专题：计算题,概率与统计
分析：该题涉及两个变量，故是与面积有关的几何概型，分别表示出满足条件的面积和整个区域的面积，最后利用概率公式解之即可．
解答：
解：由题意可得，区间[-3，3]上任取两数x，y，区域为边长为6的正方形，面积为36，
x2-y-1＜0的区域是图中阴影区域以外的部分，其面积S=
(3-x2+1)dx=
，
∴在区间[-3，3]上任取两数x，y，使x2-y-1＜0成立的概率为
=
．
故选：A．
解：由题意可得，区间[-3，3]上任取两数x，y，区域为边长为6的正方形，面积为36，x2-y-1＜0的区域是图中阴影区域以外的部分，其面积S=
| ∫ | 2 -2 |
| 32 |
| 3 |
∴在区间[-3，3]上任取两数x，y，使x2-y-1＜0成立的概率为
| ||
| 36 |
| 8 |
| 27 |
故选：A．
点评：本题主要考查了与面积有关的几何概率的求解，解题的关键是准确求出区域的面积，属于中档题．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
在一次抛硬币实验中，甲、乙两人各抛一枚硬币一次，设命题p是“甲抛的硬币正面向上”，q是“乙抛的硬币正面向上”，则命题“至少有一人抛的硬币是正面向下”可表示为（ ）
| A、（￢p）∨（￢q） |
| B、p∧（￢q） |
| C、（￢p）∧（￢q） |
| D、p∨q |
设x、y满足约束条件
，若z=x2+y2，则z的最小值为（ ）
|
A、
| ||
B、
| ||
C、
| ||
D、
|
阅读如图的程序框图，则输出的S等于（ ）
| A、-51 | B、50 |
| C、-50 | D、51 |
i是虚数单位．已知复数z=
，则复数Z对应点落在（ ）
| i-2 |
| 1-i |
| A、第四象限 | B、第三象限 |
| C、第二象限 | D、第一象限 |
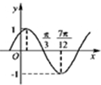
函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|＜π）的图象如图所示，则其中ω，φ分别为（ ）
A、ω=-2，φ=
| ||
B、ω=2，φ=
| ||
C、ω=2，φ=-
| ||
D、ω=-2，φ=-
|