题目内容
函数f(x)=
-
( )
| x |
| 1-2x |
| x |
| 2 |
| A、是偶函数,在(-∞,0)上是增函数 |
| B、是偶函数,在(-∞,0)上是减函数 |
| C、是奇函数,在(-∞,0)上是增函数 |
| D、是奇函数,在(-∞,0)上是减函数 |
考点:函数奇偶性的判断
专题:函数的性质及应用
分析:根据函数奇偶性的定义和单调性性质即可得到结论.
解答:
解:f(x)=
-
=x(
-
)=x•
=x•
,
函数的定义域为{x|x≠0},
则f(-x)=-x•
=-x•
=x•
=f(x),则f(x)为偶函数.
设g(x)=
=
=
-
,
当x<0时,2x是单调递增,则2x-1也是单调递增,
单调递增,则g(x)=
-
单调递增,
∵y=x也单调递增,
使用f(x)=xg(x)在在(-∞,0)上是增函数,
故选:A
| x |
| 1-2x |
| x |
| 2 |
| 1 |
| 1-2x |
| 1 |
| 2 |
| 2-1+2x |
| 2(1-2x) |
| 1+2x |
| 2(1-2x) |
函数的定义域为{x|x≠0},
则f(-x)=-x•
| 1+2-x |
| 2(1-2-x) |
| 1+2x |
| 2(2x-1) |
| 1+2x |
| 2(1-2x) |
设g(x)=
| 1+2x |
| 2(1-2x) |
| 2x-1+2 |
| 2(1-2x) |
| 1 |
| 1-2x |
| 1 |
| 2 |
当x<0时,2x是单调递增,则2x-1也是单调递增,
| 1 |
| 1-2x |
| 1 |
| 1-2x |
| 1 |
| 2 |
∵y=x也单调递增,
使用f(x)=xg(x)在在(-∞,0)上是增函数,
故选:A
点评:本题主要考查函数单调性和奇偶性的判定,利用定义法即可得到结论.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
若圆(x-3)2+(y+5)2=r2上的点到直线4x-3y-2=0的最近距离等于1,则半径r的值为( )
| A、4 | B、5 | C、6 | D、9 |
在一次抛硬币实验中,甲、乙两人各抛一枚硬币一次,设命题p是“甲抛的硬币正面向上”,q是“乙抛的硬币正面向上”,则命题“至少有一人抛的硬币是正面向下”可表示为( )
| A、(¬p)∨(¬q) |
| B、p∧(¬q) |
| C、(¬p)∧(¬q) |
| D、p∨q |
设x、y满足约束条件
,若z=x2+y2,则z的最小值为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<π)的图象如图所示,则其中ω,φ分别为( )
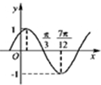

A、ω=-2,φ=
| ||
B、ω=2,φ=
| ||
C、ω=2,φ=-
| ||
D、ω=-2,φ=-
|
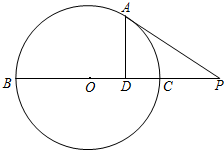 如图所示,PA与圆O相切于A,直线PO交圆O于B,C两点,AD⊥BC,垂足为D,且D是OC的中点,若PA=6,则PC=
如图所示,PA与圆O相切于A,直线PO交圆O于B,C两点,AD⊥BC,垂足为D,且D是OC的中点,若PA=6,则PC=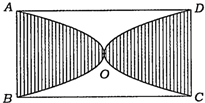 如图,矩形ABCD的面积为3,以矩形的中心O为顶点作两条抛物线,分别过点A、B和点C、D,若在矩形ABCD中随机撒入300颗豆子,则落在阴影部分内的豆子大约是
如图,矩形ABCD的面积为3,以矩形的中心O为顶点作两条抛物线,分别过点A、B和点C、D,若在矩形ABCD中随机撒入300颗豆子,则落在阴影部分内的豆子大约是