题目内容
如图所示，扇形AOB，圆心角AOB的大小等于| π |
| 3 |
 |
| AB |
（Ⅰ）若
| OA |
| 3 |
| 2 |
| CA |
（Ⅱ）设∠COP=θ，求线段CP与线段OC的长度的和的最大值及此时θ的值．
考点：正弦定理,弧度制的应用
专题：三角函数的求值
分析：（Ⅰ）由题意可得OC=1，在△OCP中由余弦定理可得PC的方程，解方程可得；（Ⅱ）在△POC中由正弦定理可用θ表示出线段CP和OC，由三角函数的知识可得．
解答：
解：（Ⅰ）∵
=
，∴OA=3OC，∴OC=1，
在△OCP中，∠OCP=
，OP=3，
由余弦定理可得OP2=OC2+PC2-2•OC•PC•cos120°，
代入数据化简可得PC2+PC-8-0，解得PC=
；
（Ⅱ）∵CP∥OB，∴∠CPO=∠POB=∠
-θ，又∠OCP=
，
在△POC中由正弦定理可得
=
=
=
，
∴CP=2
sinθ，OC=2
sin（
-θ），
∴CP+OC=2
sinθ+2
sin（
-θ）
=
sinθ+3cosθ=2
sin（
+θ），
∴当θ=
时，线段CP与线段OC的长度的和取最大值2
| OA |
| 3 |
| 2 |
| CA |
在△OCP中，∠OCP=
| 2π |
| 3 |
由余弦定理可得OP2=OC2+PC2-2•OC•PC•cos120°，
代入数据化简可得PC2+PC-8-0，解得PC=
-1+
| ||
| 2 |
（Ⅱ）∵CP∥OB，∴∠CPO=∠POB=∠
| π |
| 3 |
| 2π |
| 3 |
在△POC中由正弦定理可得
| OP |
| sin∠PCO |
| CP |
| sinθ |
| OC | ||
sin(
|
| 3 | ||
sin
|
∴CP=2
| 3 |
| 3 |
| π |
| 3 |
∴CP+OC=2
| 3 |
| 3 |
| π |
| 3 |
=
| 3 |
| 3 |
| π |
| 3 |
∴当θ=
| π |
| 6 |
| 3 |
点评：本题考查三角函数的求值和化简，涉及正弦定理和向量的应用，属中档题．
练习册系列答案
相关题目
设x、y满足约束条件
，若z=x2+y2，则z的最小值为（ ）
|
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|＜π）的图象如图所示，则其中ω，φ分别为（ ）
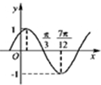
A、ω=-2，φ=
| ||
B、ω=2，φ=
| ||
C、ω=2，φ=-
| ||
D、ω=-2，φ=-
|
如图，有16个格点，每个格点小正方形的面积为1，给图中间的小正方形内任意投点P，则点P落在图中阴影部分的概率是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|