题目内容
已知函数f(x)=
(a>0).
(1)求f(x)在[
,2]上的最大值;
(2)若直线y=-x+2a为曲线y=f(x)的切线,求实数a的值;
(3)当a=2时,设x1,x2,…,x14∈[
,2],且x1+x2+…+x14=14,若不等式f(x1)+f(x2)+…+f(x14)≤λ恒成立,求实数λ的最小值.
| 9x |
| 1+ax2 |
(1)求f(x)在[
| 1 |
| 2 |
(2)若直线y=-x+2a为曲线y=f(x)的切线,求实数a的值;
(3)当a=2时,设x1,x2,…,x14∈[
| 1 |
| 2 |
考点:利用导数求闭区间上函数的最值,函数恒成立问题,利用导数研究曲线上某点切线方程
专题:综合题,导数的综合应用
分析:(1)先求f'(x),令f'(x)=0,可得极值点,分极值点在区间[
,2]内、外进行讨论可得函数的最大值;
(2)设切点为(t,f(t)),则
,解出方程组可求;
(3)f(x1)+f(x2)+…+f(x14)≤λ恒成立,等价于f(x1)+f(x2)+…+f(x14)的最大值小于等于λ.a=2时可得f(x),且由(2)知y=4-x为其切线,先由图象分析然后可证明f(x)≤4-x,由此对f(x1)+f(x2)+…+f(x14)放大,f(x1)+f(x2)+…+f(x14)≤4×14-(x1+x2+…+x14)=56-14=42,从而可求最大值,注意检验等号取得条件.
| 1 |
| 2 |
(2)设切点为(t,f(t)),则
|
(3)f(x1)+f(x2)+…+f(x14)≤λ恒成立,等价于f(x1)+f(x2)+…+f(x14)的最大值小于等于λ.a=2时可得f(x),且由(2)知y=4-x为其切线,先由图象分析然后可证明f(x)≤4-x,由此对f(x1)+f(x2)+…+f(x14)放大,f(x1)+f(x2)+…+f(x14)≤4×14-(x1+x2+…+x14)=56-14=42,从而可求最大值,注意检验等号取得条件.
解答:
解:(1)f′(x)=
=
,
令f'(x)=0,解得x=±
(负值舍去),由
<
<2,解得
<a<4.
(ⅰ)当0<a≤
时,得f'(x)≥0,∴f(x)在[
,2]上的最大值为f(2)=
.
(ⅱ)当a≥4时,由x∈[
,2],得f'(x)≤0,∴f(x)在[
,2]上的最大值为f(
)=
.
(ⅲ)当
<a<4时,∵在
<x<
时,f'(x)>0,在
<x<2时,f'(x)<0,
∴f(x)在[
,2]上的最大值为f(
)=
.
(2)设切点为(t,f(t)),则
,
由f'(t)=-1,有
=-1,化简得a2t4-7at2+10=0,即at2=2或at2=5,①
由f(t)=-t+2a,有
=2a-t,②
由①、②解得a=2或a=
.
(3)当a=2时,f(x)=
,
由(2)的结论直线y=4-x为曲线y=f(x)的切线,
∵f(2)=2,∴点(2,f(2))在直线y=4-x上,
根据图象分析,曲线y=f(x)在直线y=4-x下方.
下面给出证明:当x∈[
,2]时,f(x)≤4-x.
∵f(x)-(4-x)=
-4+x=
=
,
∴当x∈[
,2]时,f(x)-(4-x)≤0,即f(x)≤4-x.
∴f(x1)+f(x2)+…+f(x14)≤4×14-(x1+x2+…+x14),
∵x1+x2+…+x14=14,∴f(x1)+f(x2)+…+f(x14)≤56-14=42.
∴要使不等式f(x1)+f(x2)+…+f(x14)≤λ恒成立,必须λ≥42.
又当x1=x2=…=x14=1时,满足条件x1+x2+…+x14=14,且f(x1)+f(x2)+…+f(x14)=42,
因此,λ的最小值为42.
| 9[1•(1+ax2)-x•2ax] |
| (1+ax2)2 |
| 9(1-ax2) |
| (1+ax2)2 |
令f'(x)=0,解得x=±
| ||
| a |
| 1 |
| 2 |
| ||
| a |
| 1 |
| 4 |
(ⅰ)当0<a≤
| 1 |
| 4 |
| 1 |
| 2 |
| 18 |
| 4a+1 |
(ⅱ)当a≥4时,由x∈[
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 18 |
| 4+a |
(ⅲ)当
| 1 |
| 4 |
| 1 |
| 2 |
| ||
| a |
| ||
| a |
∴f(x)在[
| 1 |
| 2 |
| ||
| a |
9
| ||
| 2a |
(2)设切点为(t,f(t)),则
|
由f'(t)=-1,有
| 9(1-at2) |
| (1+at2)2 |
由f(t)=-t+2a,有
| 9t |
| 1+at2 |
由①、②解得a=2或a=
5
| |||
| 4 |
(3)当a=2时,f(x)=
| 9x |
| 1+2x2 |
由(2)的结论直线y=4-x为曲线y=f(x)的切线,
∵f(2)=2,∴点(2,f(2))在直线y=4-x上,
根据图象分析,曲线y=f(x)在直线y=4-x下方.
下面给出证明:当x∈[
| 1 |
| 2 |
∵f(x)-(4-x)=
| 9x |
| 1+2x2 |
| 2x3-8x2+10x-4 |
| 1+2x2 |
| 2(x-1)2(x-2) |
| 1+2x2 |
∴当x∈[
| 1 |
| 2 |
∴f(x1)+f(x2)+…+f(x14)≤4×14-(x1+x2+…+x14),
∵x1+x2+…+x14=14,∴f(x1)+f(x2)+…+f(x14)≤56-14=42.
∴要使不等式f(x1)+f(x2)+…+f(x14)≤λ恒成立,必须λ≥42.
又当x1=x2=…=x14=1时,满足条件x1+x2+…+x14=14,且f(x1)+f(x2)+…+f(x14)=42,
因此,λ的最小值为42.
点评:本题主要考查函数的性质、导数运算法则、导数的几何意义及其应用、不等式的求解与证明、恒成立问题,考查学生的分类讨论,计算推理能力及分析问题、解决问题的能力及创新意识.

练习册系列答案
相关题目
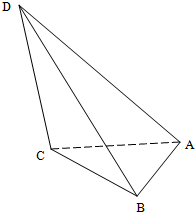 在四面体ABCD中,AB=AC=1,∠BAC=90°,AD=
在四面体ABCD中,AB=AC=1,∠BAC=90°,AD=