题目内容
已知椭圆C:
+
=1的两焦点F1(-1,0),F2(1,0),且离心率为
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)经过椭圆C的上顶点B的直线与椭圆另一个交点为A,且满足
•
=2,求△ABF2外接圆的面积.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)经过椭圆C的上顶点B的直线与椭圆另一个交点为A,且满足
| BA |
| BF2 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)由已知条件得到
,由此能求出椭圆C的标准方程.
(Ⅱ)由已知可得B(0,1),F(1,0),设A(x0,y0),由
•
=2,能求出A(0,-1)或A(
,
),由此能求出△ABF的外接圆的方程.
|
(Ⅱ)由已知可得B(0,1),F(1,0),设A(x0,y0),由
| BA |
| BF |
| 4 |
| 3 |
| 1 |
| 3 |
解答:
解:(Ⅰ)∵椭圆C:
+
=1的两焦点F1(-1,0),F2(1,0),且离心率为
,
∴
,解得a=
,c=1,b=1,
∴椭圆C的标准方程是
+y2=1.
(Ⅱ)由已知可得B(0,1),F(1,0),
设A(x0,y0),则
=(x0,y0-1),
=(1,-1),
∵
•
=2,
∴x0-(y0-1)=2,即x0=1+y0,
代入
+y02=1,得:
或
,
即A(0,-1)或A(
,
);
当A为(0,-1)时,|OA|=|OB|=|OF|=1,
△ABF的外接圆是以O为圆心,以1为半径的圆,
该外接圆的方程为x2+y2=1;
当A为(
,
)时,kBF=-1,kAF=1,
所以△ABF是直角三角形,其外接圆是以线段BA为直径的圆,
由线段BA的中点(
,
)以及|BA|=
,
得△ABF的外接圆的方程为(x-
)2+(y-
)2=
;
综上所述,△ABF的外接圆的方程为x2+y2=1或(x-
)2+(y-
)2=
.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
∴
|
| 2 |
∴椭圆C的标准方程是
| x2 |
| 2 |
(Ⅱ)由已知可得B(0,1),F(1,0),
设A(x0,y0),则
| BA |
| BF |
∵
| BA |
| BF |
∴x0-(y0-1)=2,即x0=1+y0,
代入
| x02 |
| 2 |
|
|
即A(0,-1)或A(
| 4 |
| 3 |
| 1 |
| 3 |
当A为(0,-1)时,|OA|=|OB|=|OF|=1,
△ABF的外接圆是以O为圆心,以1为半径的圆,
该外接圆的方程为x2+y2=1;
当A为(
| 4 |
| 3 |
| 1 |
| 3 |
所以△ABF是直角三角形,其外接圆是以线段BA为直径的圆,
由线段BA的中点(
| 2 |
| 3 |
| 2 |
| 3 |
2
| ||
| 3 |
得△ABF的外接圆的方程为(x-
| 2 |
| 3 |
| 2 |
| 3 |
| 5 |
| 9 |
综上所述,△ABF的外接圆的方程为x2+y2=1或(x-
| 2 |
| 3 |
| 2 |
| 3 |
| 5 |
| 9 |
点评:本题考查椭圆方程的求法,考要三角形外接圆方程的求法,是中档题,解题时要熟练掌握椭圆的简单性质,注意向量知识的合理运用.

练习册系列答案
相关题目
已知
=
,
=
,
=
且满足λ(
+
)•
=0(λ>0),则△ABC为( )
| BA |
| a |
| BC |
| b |
| AC |
| c |
| ||
|
|
| ||
|
|
| c |
| A、等腰三角形 | B、等边三角形 |
| C、直角三角形 | D、不确定 |
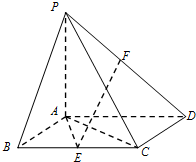 如图,已知四棱锥P-ABCD,底面ABCD为边长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点,PA=AB.
如图,已知四棱锥P-ABCD,底面ABCD为边长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点,PA=AB. 已知四面体ABCD,AD=CD,∠ADB=∠CDB=120°,且平面ABD⊥平面BCD.
已知四面体ABCD,AD=CD,∠ADB=∠CDB=120°,且平面ABD⊥平面BCD.