题目内容
已知函数f(x)=ln(x+1)+
(a∈R)
(Ⅰ)当a=2时,求函数y=f(x)的图象在x=0处的切线方程;
(Ⅱ)判断函数f(x)的单调性;
(Ⅲ)求证:ln(1+
)>
-
(n∈N*)
| ax |
| x+1 |
(Ⅰ)当a=2时,求函数y=f(x)的图象在x=0处的切线方程;
(Ⅱ)判断函数f(x)的单调性;
(Ⅲ)求证:ln(1+
| 1 |
| n |
| 1 |
| n |
| 1 |
| n2 |
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性,导数在最大值、最小值问题中的应用
专题:综合题,导数的综合应用
分析:(Ⅰ)求导函数,求出切线的斜率,再求出切点的坐标,即可得出函数y=f(x)的图象在x=0处的切线方程;
(Ⅱ)求导函数,分类讨论,利用导数的正负,可得函数f(x)的单调性;
(Ⅲ)由(Ⅱ)可知,当a=-1时,f(x)=ln(x+1)-
在(0,+∞)上单调递增.当x>0时,f(x)>f(0)=0,即ln(x+1)>
. 再令x=
,则ln(1+
)>
=
,利用
-
<
,即可的证.
(Ⅱ)求导函数,分类讨论,利用导数的正负,可得函数f(x)的单调性;
(Ⅲ)由(Ⅱ)可知,当a=-1时,f(x)=ln(x+1)-
| x |
| x+1 |
| x |
| x+1 |
| 1 |
| n |
| 1 |
| n |
| ||
|
| 1 |
| n+1 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n2 |
解答:
(Ⅰ)解:当a=2时,f(x)=ln(x+1)+
,
∴f′(x)=
,(1分)
∴f′(0)=3,∴所求的切线的斜率为3.(2分)
又∵f(0)=0,∴切点为(0,0).(3分)
故所求的切线方程为:y=3x.(4分)
(Ⅱ)解:∵f(x)=ln(x+1)+
(x>-1),
∴f′(x)=
. (6分)
①当a≥0时,∵x>-1,∴f′(x)>0; (7分)
②当a<0时,
由
,得-1<x<-1-a;由
,得x>-1-a; (8分)
综上,当a≥0时,函数f(x)在(-1,+∞)单调递增;
当a<0时,函数f(x)在(-1,-1-a)单调递减,在(-1-a,+∞)上单调递增.(9分)
(Ⅲ)证明:由(Ⅱ)可知,当a=-1时,f(x)=ln(x+1)-
在(0,+∞)上单调递增. (10分)
∴当x>0时,f(x)>f(0)=0,即ln(x+1)>
. (11分)
令x=
,则ln(1+
)>
=
. (12分)
另一方面,∵
<
,即
-
<
,
∴
>
-
,(13分)
∴ln(1+
)>
-
(n∈N*)(14分)
| 2x |
| x+1 |
∴f′(x)=
| x+3 |
| (x+1)2 |
∴f′(0)=3,∴所求的切线的斜率为3.(2分)
又∵f(0)=0,∴切点为(0,0).(3分)
故所求的切线方程为:y=3x.(4分)
(Ⅱ)解:∵f(x)=ln(x+1)+
| ax |
| x+1 |
∴f′(x)=
| x+1+a |
| (x+1)2 |
①当a≥0时,∵x>-1,∴f′(x)>0; (7分)
②当a<0时,
由
|
|
综上,当a≥0时,函数f(x)在(-1,+∞)单调递增;
当a<0时,函数f(x)在(-1,-1-a)单调递减,在(-1-a,+∞)上单调递增.(9分)
(Ⅲ)证明:由(Ⅱ)可知,当a=-1时,f(x)=ln(x+1)-
| x |
| x+1 |
∴当x>0时,f(x)>f(0)=0,即ln(x+1)>
| x |
| x+1 |
令x=
| 1 |
| n |
| 1 |
| n |
| ||
|
| 1 |
| n+1 |
另一方面,∵
| 1 |
| n(n+1) |
| 1 |
| n2 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n2 |
∴
| 1 |
| n+1 |
| 1 |
| n |
| 1 |
| n2 |
∴ln(1+
| 1 |
| n |
| 1 |
| n |
| 1 |
| n2 |
点评:本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性,考查不等式的证明,正确运用导数是关键.

练习册系列答案
相关题目
一个几何体的三视图如图所示,则该几何体的体积为( )
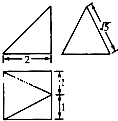

A、
| ||||
B、
| ||||
C、4
| ||||
D、
|
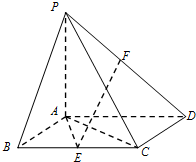 如图,已知四棱锥P-ABCD,底面ABCD为边长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点,PA=AB.
如图,已知四棱锥P-ABCD,底面ABCD为边长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点,PA=AB. 某网络营销部门为了统计某市网友2013年11月11日在某淘宝店的网购情况,随机抽查了该市当天60名网友的网购金额情况,得到如下数据统计表(如表):
某网络营销部门为了统计某市网友2013年11月11日在某淘宝店的网购情况,随机抽查了该市当天60名网友的网购金额情况,得到如下数据统计表(如表):