题目内容
给出以下结论：
①在四边形ABCD中，若
=
+
，则ABCD是平行四边形；
②在三角形ABC中，若a=5，b=8，C=60°，则
•
=20；
③已知正方形ABCD的边长为l，则|
+
+
|=2
；
④已知
=a+5b，
=2a+8b，
=3(a-b)，则A，B，C三点共线．
其中正确结论的个数为（ ）
①在四边形ABCD中，若
| AC |
| AB |
| AD |
②在三角形ABC中，若a=5，b=8，C=60°，则
| BC |
| CA |
③已知正方形ABCD的边长为l，则|
| AB |
| BC |
| AC |
| 2 |
④已知
| AB |
| BC |
| CD |
其中正确结论的个数为（ ）
| A、1 | B、2 | C、3 | D、4 |
考点：命题的真假判断与应用
专题：平面向量及应用
分析：必须对选项一一加以判断：对①运用向量加法的平行四边形法则；对②应用向量的数量积定义加以判断；
对③运用向量的加法和模的概念解决；对④运用向量的共线知识解决．
对③运用向量的加法和模的概念解决；对④运用向量的共线知识解决．
解答：
解：由向量的加法满足的平行四边形法则可知，选项①对；
对②，因为在三角形ABC中，a=5，b=8，C=60°，所以
•
=abcos(π-C)=5×8×（-cos60°）
=40×（-
）=-20，故②错；
对③，因为正方形ABCD的边长为l，所以|
+
+
|=2|
|=
，故③对；
对④，因为
=a+5b，
=2a+8b，所以不存在实数λ，使得
=λ
，即
，
不共线，
所以点A，B，C不共线，故④错．
故选：B．
对②，因为在三角形ABC中，a=5，b=8，C=60°，所以
| BC |
| CA |
=40×（-
| 1 |
| 2 |
对③，因为正方形ABCD的边长为l，所以|
| AB |
| BC |
| AC |
| AC |
| 2 |
对④，因为
| AB |
| BC |
| AB |
| BC |
| AB |
| BC |
所以点A，B，C不共线，故④错．
故选：B．
点评：本题主要考查平面向量及其运用，特别注意运用向量的数量积定义，要注意两向量的夹角，由向量共线可推到点共线，本题是一道基础题．
练习册系列答案
相关题目
一个几何体的三视图如图所示，则该几何体的体积为（ ）
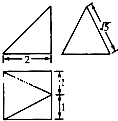
A、
| ||||
B、
| ||||
C、4
| ||||
D、
|
若集合A满足：对任意x∈A，都有
∈A，就称A是和谐集合．则在集合M={-1，0，
，
，
，1，2，3，4，5，6}的所有非空子集中，和谐集合有（ ）个．
| 1 |
| x |
| 1 |
| 5 |
| 1 |
| 3 |
| 1 |
| 2 |
| A、255 | B、127 |
| C、63 | D、31 |
已知
=
，
=
，
=
且满足λ（
+
）•
=0（λ＞0），则△ABC为（ ）
| BA |
| a |
| BC |
| b |
| AC |
| c |
| ||
|
|
| ||
|
|
| c |
| A、等腰三角形 | B、等边三角形 |
| C、直角三角形 | D、不确定 |