题目内容
“0≤k<3”是方程
+
=1表示双曲线的( )
| x2 |
| k+1 |
| y2 |
| k-5 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
考点:双曲线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:“0≤k<3”⇒方程
+
=1表示双曲线;反之,方程
+
=1表示双曲线-1<k<5.由此得到“0≤k<3”是方程
+
=1表示双曲线的充分不必要条件.
| x2 |
| k+1 |
| y2 |
| k-5 |
| x2 |
| k+1 |
| y2 |
| k-5 |
| x2 |
| k+1 |
| y2 |
| k-5 |
解答:
解:∵0≤k<3,∴
,
∴方程
+
=1表示双曲线;
反之,∵方程
+
=1表示双曲线,
∴(k+1)(k-5)<0,
解得-1<k<5.
∴“0≤k<3”是方程
+
=1表示双曲线的充分不必要条件.
故选:A.
|
∴方程
| x2 |
| k+1 |
| y2 |
| k-5 |
反之,∵方程
| x2 |
| k+1 |
| y2 |
| k-5 |
∴(k+1)(k-5)<0,
解得-1<k<5.
∴“0≤k<3”是方程
| x2 |
| k+1 |
| y2 |
| k-5 |
故选:A.
点评:本题考查命题真假的判断,是基础题,解题时要认真审题,注意双曲线的简单性质的合理运用.

练习册系列答案
相关题目
若a=sin(cosπx),b=cos(sinπx)且x∈[-
,-1],则( )
| 3 |
| 2 |
| A、a2+b2=1 |
| B、a<b |
| C、a>b |
| D、a=b |
已知集合D={x|
>0},若a,b∈D且
+
=
,则9a•3b的最小值为( )
| 24-x |
| x-9 |
| 1 |
| a |
| 1 |
| 2b |
| 1 |
| 12 |
| A、27 |
| B、327 |
| C、54 |
| D、354 |
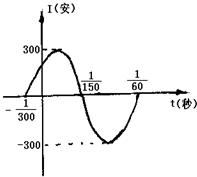 如图,表示电流强度I与时间t的关系式I=Asin(ωt+φ)(A>0,ω>0),在一个周期内的图象.
如图,表示电流强度I与时间t的关系式I=Asin(ωt+φ)(A>0,ω>0),在一个周期内的图象.