题目内容
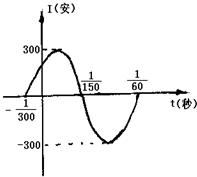 如图,表示电流强度I与时间t的关系式I=Asin(ωt+φ)(A>0,ω>0),在一个周期内的图象.
如图,表示电流强度I与时间t的关系式I=Asin(ωt+φ)(A>0,ω>0),在一个周期内的图象.(1)试根据图象写出I=Asin(ωt+φ)的解析式;
(2)为了使I=Asin(ωt+φ)中t在任意一段
| 1 |
| 100 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的图象
专题:三角函数的图像与性质
分析:(1)根据函数的图象确定A,ω 和φ的值即可.
(2)根据条件则函数周期满足周期T≤
,解不等式即可得到结论.
(2)根据条件则函数周期满足周期T≤
| 1 |
| 100 |
解答:
解:(1)由图象可知A=300,
函数的周期T=
-(-
)=
,
即
=
,则ω=100π,
由五点对应法知-
ω+φ=0,
解得φ=
,
∴f(x)=300sin(100πt+
).
(2)要使t在任意一段
秒能取得最大值和最小值,必须使得周期T≤
即
≤
,
即≥200π≈628
由于ω为正整数,
故ω的最小值为:629
函数的周期T=
| 1 |
| 60 |
| 1 |
| 300 |
| 1 |
| 50 |
即
| 2π |
| ω |
| 1 |
| 50 |
由五点对应法知-
| 1 |
| 300 |
解得φ=
| π |
| 3 |
∴f(x)=300sin(100πt+
| π |
| 3 |
(2)要使t在任意一段
| 1 |
| 100 |
| 1 |
| 100 |
即
| 2π |
| ω |
| 1 |
| 100 |
即≥200π≈628
由于ω为正整数,
故ω的最小值为:629
点评:本题主要考查函数解析式的求解以及周期的应用,根据条件确定A,ω 和φ的值是解决本题的关键.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
y=2sin(2x-
) 的振幅、频率和初相分别为( )
| π |
| 4 |
A、2,
| ||||
B、2,
| ||||
C、2,
| ||||
D、2,
|
已知x,y>0,xy+1=2x-y,若对于满足条件的任意x,y有(x+y)2-a(x+y)+1≥0恒成立,则a的取值范围是( )
| A、[-2,2] | ||
B、(-∞,
| ||
| C、(-∞,2] | ||
D、[2,
|
命题p:?x∈Z,则x2-4>0;与命题q:?x∈Z,使x2-4>0,下列结论正确的是( )
| A、p真q假 | B、p假q真 |
| C、p∧q为真 | D、p∨q为假 |
“0≤k<3”是方程
+
=1表示双曲线的( )
| x2 |
| k+1 |
| y2 |
| k-5 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |