题目内容
已知二次函数f(x)=x2-2(2m-1)x+5m2-2m+4在[0,1]上的最小值为g(m);
(1)求g(m)的解析式;
(2)若m∈[-2,0],设g(m)的最小值为M,计算log19
(1+log5M)的值.
(1)求g(m)的解析式;
(2)若m∈[-2,0],设g(m)的最小值为M,计算log19
| 5 |
考点:二次函数在闭区间上的最值,函数解析式的求解及常用方法
专题:函数的性质及应用
分析:(1)二次函数f(x)的图象的对称轴为x=2m-1,再分对称轴在所给区间的左侧、中间、右侧三种情况,分别求得f(x)的最小值为g(m)的解析式,综合可得结论.
(2)根据m∈[-2,0],则g(m)为减函数,求得g(m)的最小值为M=4,再利用对数的运算性质,求得log19
(1+log5M)的值.
(2)根据m∈[-2,0],则g(m)为减函数,求得g(m)的最小值为M=4,再利用对数的运算性质,求得log19
| 5 |
解答:
解:(1)二次函数f(x)=x2-2(2m-1)x+5m2-2m+4的图象的对称轴为x=2m-1,
当2m-1<0 时,即m<
时,f(x)在[0,1]上单调递增,f(x)的最小值为g(m)=f(0)=5m2-2m+4;
当2m-1∈[0,1]时,即m∈[
,1]时,f(x)在[0,2m-1]上单调递减,在[2m-1],1]上单调递增,f(x)的最小值为g(m)=f(2m-1)=m2+2m+3;
当2m-1>1 时,即m>1时,f(x)在[0,1]上单调递减,f(x)的最小值为g(m)=f(1)=5m2-6m+7,
故g(m)=
.
(2)若m∈[-2,0],则g(m)=5m2-2m+4为减函数,故g(m)的最小值为M=g(0)=4,
log19
(1+log5M)=log19
+log19
•log54=log19
+log19
•log
2=log19(
×2)=log19(2
).
当2m-1<0 时,即m<
| 1 |
| 2 |
当2m-1∈[0,1]时,即m∈[
| 1 |
| 2 |
当2m-1>1 时,即m>1时,f(x)在[0,1]上单调递减,f(x)的最小值为g(m)=f(1)=5m2-6m+7,
故g(m)=
|
(2)若m∈[-2,0],则g(m)=5m2-2m+4为减函数,故g(m)的最小值为M=g(0)=4,
log19
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
点评:本题主要考查求二次函数在闭区间上的最值,二次函数的性质的应用,对数的运算性质,体现了分类讨论的数学思想,属基础题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
已知双曲线的渐近线为y=±
x,焦点坐标为(-4,0),(4,0),则双曲线方程为( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
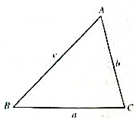 如图所示,△ABC的三边分别为a、b、c.
如图所示,△ABC的三边分别为a、b、c.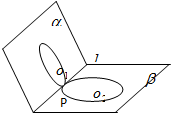 如图,在120°二面角α-l-β内半径为1的圆O1与半径为2的圆α分别在半平面α、l内,且与棱l切于同一点P,则以圆O1与圆f(x)=2sin(ωx-
如图,在120°二面角α-l-β内半径为1的圆O1与半径为2的圆α分别在半平面α、l内,且与棱l切于同一点P,则以圆O1与圆f(x)=2sin(ωx-