题目内容
比较tan（-
）与tan（-
）的大小．
| 17π |
| 4 |
| 22π |
| 5 |
考点：正切函数的单调性,运用诱导公式化简求值
专题：三角函数的求值,三角函数的图像与性质
分析：利用诱导公式化简函数的表达式，自变量在正切函数的同一个单调区间内，即可判断大小．
解答：
解：tan（-
）=-tan
，
tan（-
）=-tan
，
＞
，tan
＞tan
，
所以tan（-
）＜tan（-
）．
| 17π |
| 4 |
| π |
| 4 |
tan（-
| 22π |
| 5 |
| 2π |
| 5 |
| 2π |
| 5 |
| π |
| 4 |
| 2π |
| 5 |
| π |
| 4 |
所以tan（-
| 17π |
| 4 |
| 22π |
| 5 |
点评：本题考查诱导公式的应用，正切函数的单调性，基本知识的考查．
练习册系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
（理做）已知函数f（x）=log2015（x+1），a=2017，b=2016，c=2015，则
，
，
的大小关系是（ ）
| f(a) |
| a |
| f(b) |
| b |
| f(c) |
| c |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
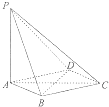如图，在四棱锥P-ABCD中，PA丄平面ABCD，底面ABCD是菱形AB=2，∠BAD=60°．