题目内容
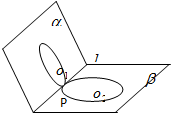 如图,在120°二面角α-l-β内半径为1的圆O1与半径为2的圆α分别在半平面α、l内,且与棱l切于同一点P,则以圆O1与圆f(x)=2sin(ωx-
如图,在120°二面角α-l-β内半径为1的圆O1与半径为2的圆α分别在半平面α、l内,且与棱l切于同一点P,则以圆O1与圆f(x)=2sin(ωx-| π |
| 6 |
| π |
| 3 |
考点:与二面角有关的立体几何综合题
专题:计算题,空间位置关系与距离
分析:由题意设球心到圆O1的距离为x,到半径为2的圆O的距离为y,球的半径为R,从而可得x2+1=R2,y2+4=R2,再由解三角形可得x2+y2-xy=7,从而求出R2,进而求表面积.
解答:
解:设球心到圆O1的距离为x,到半径为2的圆O的距离为y,
球的半径为R,则
x2+1=R2,
y2+4=R2,
又∵二面角α-l-β为120°,且两圆与棱l切于同一点P,
∴解三角形可得,
x2+y2-2xycos60°=12+22-2×1×2×cos120°,
即x2+y2-xy=7,
联立可得,
,
解得,R2=
,x=
,y=
,
故球的表面积S=4πR2=
;
故答案为:
.
球的半径为R,则
x2+1=R2,
y2+4=R2,
又∵二面角α-l-β为120°,且两圆与棱l切于同一点P,
∴解三角形可得,
x2+y2-2xycos60°=12+22-2×1×2×cos120°,
即x2+y2-xy=7,
联立可得,
|
解得,R2=
| 28 |
| 3 |
5
| ||
| 3 |
4
| ||
| 3 |
故球的表面积S=4πR2=
| 112π |
| 3 |
故答案为:
| 112π |
| 3 |
点评:本题考查了球的几何结构,同时考查了学生的空间想象力与化简计算的能力,属于难题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
已知焦点在y轴上的椭圆
+
=1的长轴长为8,则m等于( )
| x2 |
| 10 |
| y2 |
| m |
| A、4 | B、8 | C、10 | D、16 |
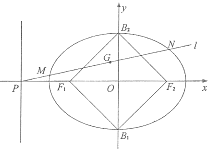 如图,已知椭圆C的中心在原点,焦点在x轴上,以两个焦点和短轴的两个端点为顶点的四边形F1B1F2B2是一个面积为8的正方形(记为Q ).
如图,已知椭圆C的中心在原点,焦点在x轴上,以两个焦点和短轴的两个端点为顶点的四边形F1B1F2B2是一个面积为8的正方形(记为Q ). 如图,四棱锥P-ABCD中,底面ABCD为是矩形,PA⊥底面ABCD,E为棱PD的中点,AP=2,AD=
如图,四棱锥P-ABCD中,底面ABCD为是矩形,PA⊥底面ABCD,E为棱PD的中点,AP=2,AD=