题目内容

直线l1：x-2y-2=0关于直线l2：x+y=0对称的直线l3的方程为
 
．
考点：与直线关于点、直线对称的直线方程
专题：直线与圆
分析：可求得直线l1：x-2y-2=0与两坐标轴交点的坐标A（0，-1）与B（2，0），再分别求得这两点关于直线l2：x+y=0对称点的坐标，即可求得线l3的方程．
解答： 解：对于直线l1：x-2y-2=0，
当x=0时，y=-1，即该直线经过A（0，-1）；
当y=0时，x=2，即该直线经过B（2，0）；
∵点A（0，-1）关于直线l2：x+y=0对称点A′的坐标为A′（1，0）；
点B（2，0）关于直线l2：x+y=0对称点B′的坐标为B′（0，-2）；
∴直线l1：x-2y-2=0关于直线l2：x+y=0对称的直线l3的方程为：y-0=
0-(-2)
1-0
（x-1），
整理得：2x-y-2=0．
故答案为：
点评：本题考查与直线关于点、直线对称的直线方程，求得直线l1：x-2y-2=0与两坐标轴的两交点关于直线l2：x+y=0对称点的坐标是关键，考查运算能力，题目难度中档．
练习册系列答案
相关题目
设全集U={-1，0，1，2，3，4，5}，集合A={1，2}，集合B={0，1}，分别求集合∁UA；  A∪B； A∩B．
设x，y均为正数，且x＞y，求证：2x+
1
x2-2xy+y2
≥2y+3．
设抛物线x2=2py（p＞0）的焦点F，过焦点F作y轴的垂线，交抛物线于A、B两点，点M（0，-
p
2
），Q为抛物线上异于A、B的任意一点，经过点Q作抛物线的切线，记为l，l与MA、MB分别交于D、E．
（Ⅰ）求证：直线MA、MB与抛物线相切；
（Ⅱ）求证
S△QAB
S△MDC
=2．
已知椭圆C：
x2 
a2
+
y2
b2
═1的左右焦点为F1，F2，e=
1
3
过F1的直线l交椭圆C于A、B两点，|AF2||AB||BF2|成等差数列，|AB|=4．
（1）求椭圆C的方程．
（2）M、N是椭圆C上的两点，若MN被直线x=1平分，证明MN的中垂线过定点．
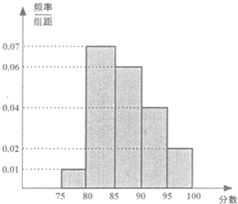一企业某次招聘新员工分笔试和面试两部分，人力资源部经理把参加笔试的40名学生的成绩分组：第1组[75，80），第2组[80，85），第3组[85，90），第4组[90，95），第5组[95，100），得到频率分布直方图如图所示．
（Ⅰ）分别求成绩在第4，5组的人数；
（Ⅱ）若该经理决定在笔试成绩较高的第3，4，5组中用分层抽样抽取6名进入面试，
①已知甲和乙的成绩均在第3组，求甲和乙同时进入面试的概率；
②若经理决定在这6名学生中随机抽取2名学生接受考官D的面试，设第4组中有X名学生被考官D面试，求X的分布列和数学期望．
已知向量
a
，
b
为单位向量，且
a
•
b
=-
1
2
，向量
c
与
a
+
b
共线，则|
a
+
c
|的最小值为
 
．
已知函数f（x）=x2-2x-1，x∈A当为下列区间时，分别求f（x）的最大值和最小值，
（1）A=[-2，0]；
（2）A=[-1，2]；
（3）A=[2，3]．
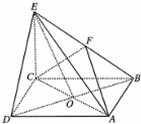在四棱锥E-ABCD中，底面ABCD是正方形，AC与BD交于点O，EC⊥底面ABCD，F为BE的中点．
（1）求证：DE∥平面ACF；
（2）若CE=1，AB=
2
，求三棱锥E-ACF的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网