Question

设抛物线x²=2py（p＞0）的焦点F，过焦点F作y轴的垂线，交抛物线于A、B两点，点M（0，-

p

2

），Q为抛物线上异于A、B的任意一点，经过点Q作抛物线的切线，记为l，l与MA、MB分别交于D、E．
（Ⅰ）求证：直线MA、MB与抛物线相切；
（Ⅱ）求证

S△QAB

S△MDC

=2．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：综合题,圆锥曲线的定义、性质与方程

分析：（Ⅰ）求出l_AM：y=-x-

p

2

，l_MB：y=x-

p

2

，代入x²=2py，利用根的判别式，可得直线MA、MB与抛物线相切；
（Ⅱ）求出S_△QAB=

|x12-p2|

2

，S_△MDC=

1

2

p2+x12

•

|x12-p2|

2 x12+p2

=

|x12-p2|

4

，即可证明结论．

解答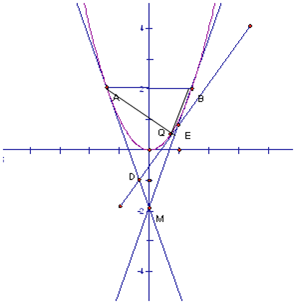： （Ⅰ）解：y_A=y_B=

p

2

，x_A=-p，x_B=p---------（1分）
k_AM=-1．k_MB=-1---------（2分）
l_AM：y=-x-

p

2

，l_MB：y=x-

p

2

---------（3分）
l_AM：y=-x-

p

2

，代入x²=2py，可得x²+2px+p=0，
∴△=0
∴直线AM与抛物线相切，
同理直线BM与抛物线相切---------（5分）
（Ⅱ）证明：设Q（x₁，y₁），切线l：=

x1

p

x-

x12

2p

，S_△QAB=

|x12-p2|

2

---------（7分）
l_AM：y=-x-

p

2

与切线l：=

x1

p

x-

x12

2p

联立，
可得D（

x1-p

2

，-

x1

2

），
同理E（

x1+p

2

，

x1

2

），---------（10分）
∴|DE|=

p2+x12

，
∵M到直线DE的距离d=

|x12-p2|

2 x12+p2

--------（12分）
∴S_△MDC=

1

2

p2+x12

•

|x12-p2|

2 x12+p2

=

|x12-p2|

4

∴

S△QAB

S△MDC

=2．---------（13分）

点评：本题考查直线与抛物线的位置关系，考查三角形面积的计算，考查学生分析解决问题的能力，属于中档题．