题目内容
已知椭圆C:
+
═1的左右焦点为F1,F2,e=
过F1的直线l交椭圆C于A、B两点,|AF2||AB||BF2|成等差数列,|AB|=4.
(1)求椭圆C的方程.
(2)M、N是椭圆C上的两点,若MN被直线x=1平分,证明MN的中垂线过定点.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 3 |
(1)求椭圆C的方程.
(2)M、N是椭圆C上的两点,若MN被直线x=1平分,证明MN的中垂线过定点.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知得4a=|AF2|+|AF1|+|BF2|+|BF1|=|AF2|+|BF2|+|AB|=3|AB|=12,e=
=
,由此能求出椭圆方程.
(Ⅱ)设M(x1,y1),N(x2,y2),MN的中点为(1,y0),利用点差法求出线段MN的中垂线方程为y-y0=
(x-1),由此能证明MN的中垂线过定点(
,0).
| c |
| a |
| 1 |
| 3 |
(Ⅱ)设M(x1,y1),N(x2,y2),MN的中点为(1,y0),利用点差法求出线段MN的中垂线方程为y-y0=
| 9y0 |
| 8 |
| 1 |
| 9 |
解答:
(Ⅰ)解:∵|AF2|、|AB|、|BF2|成等差数列,
∴|AF2|+|BF2|=2|AB|.…2分
∴4a=|AF2|+|AF1|+|BF2|+|BF1|=|AF2|+|BF2|+|AB|=3|AB|=12,…5分
得a=3,又e=
=
,所以c=1,b=
=2
,
所求的椭圆方程为:
+
=1.…7分
(Ⅱ)证明:设M(x1,y1),N(x2,y2),MN的中点为(1,y0),
由题意知:
+
=1,
+
=1,…9分
两式相减得:
+
=0,
∴kMN=
=-
=-
,
所以线段MN的中垂线方程为y-y0=
(x-1),…11分
∴此直线经过定点(
,0).
∴MN的中垂线过定点(
,0).…12分
∴|AF2|+|BF2|=2|AB|.…2分
∴4a=|AF2|+|AF1|+|BF2|+|BF1|=|AF2|+|BF2|+|AB|=3|AB|=12,…5分
得a=3,又e=
| c |
| a |
| 1 |
| 3 |
| a2-c2 |
| 2 |
所求的椭圆方程为:
| x2 |
| 9 |
| y2 |
| 8 |
(Ⅱ)证明:设M(x1,y1),N(x2,y2),MN的中点为(1,y0),
由题意知:
| x12 |
| 9 |
| y12 |
| 8 |
| x22 |
| 9 |
| y22 |
| 8 |
两式相减得:
| (x1+x2)(x1-x2) |
| 9 |
| (y1+y2)(y1-y2) |
| 8 |
∴kMN=
| y1-y2 |
| x1-x2 |
| 8(x1+x2) |
| 9(y1+y2) |
| 8 |
| 9y0 |
所以线段MN的中垂线方程为y-y0=
| 9y0 |
| 8 |
∴此直线经过定点(
| 1 |
| 9 |
∴MN的中垂线过定点(
| 1 |
| 9 |
点评:本题考查椭圆方程的求法,考查线段的中垂线过定点的证明,是中档题,解题时要认真审题,注意椭圆方程的性质的合理运用.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
已知集合M={-1,0,2},N={x|
≤0},则M∩N=( )
| x-2 |
| x+1 |
| A、{-1,0,2} |
| B、{0,1,2} |
| C、{0,2} |
| D、∅ |
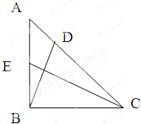 等腰直角三角形ABC中,AB=BC=2,
等腰直角三角形ABC中,AB=BC=2,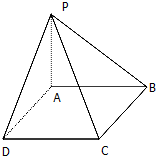 如图,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,PA=1,PD=
如图,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,PA=1,PD=