题目内容
已知函数f(x)=x2-2x-1,x∈A当为下列区间时,分别求f(x)的最大值和最小值,
(1)A=[-2,0];
(2)A=[-1,2];
(3)A=[2,3].
(1)A=[-2,0];
(2)A=[-1,2];
(3)A=[2,3].
考点:二次函数在闭区间上的最值
专题:函数的性质及应用
分析:根据二次函数的性质,确定函数的单调区间,从而求出函数的最值问题.
解答:
解:∵f(x)=x2-2x-1=(x-1)2-2,
函数开口向上,对称轴x=1,
∴(1)在A=[-2,0]上,f(x)递减,
∴f(x)min=f(0)=-1,f(x)max=f(-2)=7;
(2)在A=[-1,2]上,f(x)在[-1,1)递减,在(1,2]递增,
∴f(x)min=f(1)=-2,f(x)max=f(-1)=2,
(3)在A=[2,3]上,f(x)递增,
∴f(x)min=f(2)=-1,f(x)max=f(3)=2.
函数开口向上,对称轴x=1,
∴(1)在A=[-2,0]上,f(x)递减,
∴f(x)min=f(0)=-1,f(x)max=f(-2)=7;
(2)在A=[-1,2]上,f(x)在[-1,1)递减,在(1,2]递增,
∴f(x)min=f(1)=-2,f(x)max=f(-1)=2,
(3)在A=[2,3]上,f(x)递增,
∴f(x)min=f(2)=-1,f(x)max=f(3)=2.
点评:本题考查了二次函数的性质,函数的单调性,函数的最值问题,是一道基础题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
如图:底面是矩形ABCD,PA⊥底面ABCD,则图中直角三角形的个数( )
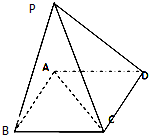

| A、8 | B、7 | C、6 | D、5 |
数列{an}前n项和Sn=n2+2n-2,对数列{an}的描述正确的是( )
| A、数列{an}为递增数列 |
| B、数列{an}为递减数列 |
| C、数列{an}为等差数列 |
| D、数列{an}为等比数列 |