题目内容
已知函数r(x)=lnx,函数h(x)=
(1-
)(a>0),f(x)=r(x)-h(x).
(Ⅰ)试求f(x)的单调区间.
(Ⅱ)若f(x)在区间[1,+∞)上是单调递增函数,试求实数a的取值范围:
(Ⅲ)设数列{an}是公差为1.首项为l的等差数列,数列{
}的前n项和为Sn,求证:当a=1时,Sn-2<f(n)-
<Sn-1-1(n∈N*,n≥2).
| 1 |
| a |
| 1 |
| x |
(Ⅰ)试求f(x)的单调区间.
(Ⅱ)若f(x)在区间[1,+∞)上是单调递增函数,试求实数a的取值范围:
(Ⅲ)设数列{an}是公差为1.首项为l的等差数列,数列{
| 1 |
| an |
| 1 |
| n |
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的单调性,数列与不等式的综合
专题:导数的综合应用
分析:(Ⅰ)利用导数法判断函数的单调性,求得单调区间;
(Ⅱ)由导数与函数单调性的关系,若f(x)在x∈[1,+∞)是单调递增函数,则f′(x)≥0恒成立,即a≥(
)max,利用(1)的结论求得结论;
(Ⅲ)构造函数g(x)=x-1-lnx,利用导数证得lnx<x-1,所以x∈(1,+∞)时,ln
<
-1=
,又由(Ⅱ)可得
f(x)>f(1),所以
+lnx>0,即lnx>1-
,所以ln
>1-
=
;故有不等式
<ln
<
成立.
令x=1,2,…,n-1,(n∈N*且n≥2),即可得证.
(Ⅱ)由导数与函数单调性的关系,若f(x)在x∈[1,+∞)是单调递增函数,则f′(x)≥0恒成立,即a≥(
| 1 |
| x |
(Ⅲ)构造函数g(x)=x-1-lnx,利用导数证得lnx<x-1,所以x∈(1,+∞)时,ln
| x+1 |
| x |
| x+1 |
| x |
| 1 |
| x |
f(x)>f(1),所以
| 1-x |
| x |
| 1 |
| x |
| x+1 |
| x |
| 1 | ||
|
| 1 |
| x+1 |
| 1 |
| x+1 |
| x+1 |
| x |
| 1 |
| x |
令x=1,2,…,n-1,(n∈N*且n≥2),即可得证.
解答:
解:(Ⅰ)f(x)=lnx-
(1-
),则f′(x)=
,
∵a>0,x>0,所以ax2>0,令ax-1>0,x>
,
∴f(x)的单调递增区间是(
,+∞);
f(x)的单调递减区间是(0,
);…(4分)
(Ⅱ)若f(x)在x∈[1,+∞)是单调递增函数,则f′(x)≥0恒成立,即a≥
恒成立
即a≥(
)max,
∵x∈[1,+∞),
∴
≤1,故a≥1.….(7分)
(Ⅲ)设数列{an}是公差为1首项为1的等差数列,所以an=n,Sn=1+
+…+
,
当a=1时,由(Ⅱ)知:f(x)=
+lnx在x∈[1,+∞)上为增函数,f(n)-
=lnn-1,
当x>1时,f(x)>f(1),所以
+lnx>0,即lnx>1-
,
∴ln
>1-
=
;
令g(x)=x-1-lnx,则有g′(x)=1-
,当x∈(1,+∞),有g′(x)>0
则g(x)>g(1)=0,即lnx<x-1,所以x∈(1,+∞)时,ln
<
-1=
∴不等式
<ln
<
成立.
令x=1,2,…,n-1,(n∈N*且n≥2)时,
将所得各不等式相加,得
+
+…+
<ln
+ln
+…+ln
<1+
+…+
,
即
+
+…+
<lnn<1+
+…+
.
∴Sn-2<f(n)-
<Sn-1-1(n∈N*且n≥2). …(13分)
| 1 |
| a |
| 1 |
| x |
| ax-1 |
| ax2 |
∵a>0,x>0,所以ax2>0,令ax-1>0,x>
| 1 |
| a |
∴f(x)的单调递增区间是(
| 1 |
| a |
f(x)的单调递减区间是(0,
| 1 |
| a |
(Ⅱ)若f(x)在x∈[1,+∞)是单调递增函数,则f′(x)≥0恒成立,即a≥
| 1 |
| x |
即a≥(
| 1 |
| x |
∵x∈[1,+∞),
∴
| 1 |
| x |
(Ⅲ)设数列{an}是公差为1首项为1的等差数列,所以an=n,Sn=1+
| 1 |
| 2 |
| 1 |
| n |
当a=1时,由(Ⅱ)知:f(x)=
| 1-x |
| x |
| 1 |
| n |
当x>1时,f(x)>f(1),所以
| 1-x |
| x |
| 1 |
| x |
∴ln
| x+1 |
| x |
| 1 | ||
|
| 1 |
| x+1 |
令g(x)=x-1-lnx,则有g′(x)=1-
| 1 |
| x |
则g(x)>g(1)=0,即lnx<x-1,所以x∈(1,+∞)时,ln
| x+1 |
| x |
| x+1 |
| x |
| 1 |
| x |
∴不等式
| 1 |
| x+1 |
| x+1 |
| x |
| 1 |
| x |
令x=1,2,…,n-1,(n∈N*且n≥2)时,
将所得各不等式相加,得
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 2 |
| 1 |
| 3 |
| 2 |
| n |
| n-1 |
| 1 |
| 2 |
| 1 |
| n-1 |
即
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| n-1 |
∴Sn-2<f(n)-
| 1 |
| n |
点评:本题主要考查利用导数研究函数的单调性、求函数的最值知识,考查恒成立问题及证明利用函数证明不等式成立问题的能力,考查转化划归思想及构造函数法的运用能力,逻辑思维强,属难题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
已知A={x|log2x<2},B={x|
<3x<
},则A∩B为( )
| 1 |
| 3 |
| 3 |
A、(0,
| ||
B、(0,
| ||
C、(-1,
| ||
D、(-1,
|
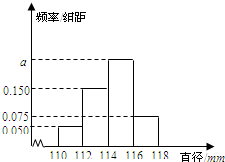 某工厂生产的产品A的直径均位于区间[110,118]内(单位:mm).若生产一件产品A的直径位于区间[110,112],[112,114],[114,116],[116,118]内该厂可获利分别为10,20,30,10(单位:元),现从该厂生产的产品A中随机100件测量它们的直径,得到如图所示的频率分布直方图.
某工厂生产的产品A的直径均位于区间[110,118]内(单位:mm).若生产一件产品A的直径位于区间[110,112],[112,114],[114,116],[116,118]内该厂可获利分别为10,20,30,10(单位:元),现从该厂生产的产品A中随机100件测量它们的直径,得到如图所示的频率分布直方图. 已知:△AOB中,∠AOB=90°,AO=h,OB=r,如图所示,先将△AOB绕AO所在直线旋转一周得到一个圆锥,再在该圆锥内旋转一个长宽都为
已知:△AOB中,∠AOB=90°,AO=h,OB=r,如图所示,先将△AOB绕AO所在直线旋转一周得到一个圆锥,再在该圆锥内旋转一个长宽都为