Question

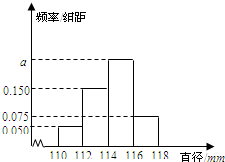某工厂生产的产品A的直径均位于区间[110，118]内（单位：mm）．若生产一件产品A的直径位于区间[110，112]，[112，114]，[114，116]，[116，118]内该厂可获利分别为10，20，30，10（单位：元），现从该厂生产的产品A中随机100件测量它们的直径，得到如图所示的频率分布直方图．
（Ⅰ）求a的值，并估计该厂生产一件A产品的平均利润；
（Ⅱ）现用分层抽样法从直径位于区间[112，116）内的产品中随机抽取一个容量为5的样
本，再从样本中随机抽取两件产品进行检测，求两件产品中至少有一件产品的直径位于区间[114，116）内的概率．

Answer 1

考点：分层抽样方法,古典概型及其概率计算公式

专题：计算题,概率与统计

分析：（I）利用所有小矩形的面积之和为1求得a值；根据频数=频率×样本容量求得各组的频数，代入平均数公式计算；
（II）根据频率分布直方图求得直径位于区间[112，114）和[114，116）的频率之比，可得在两组中应取的产品数，
利用写出所有基本事件的方法求符合条件的基本事件个数比；

解答： 解：（I）由频率分布直方图得：2×（0.050+0.150+a+0.075）=1⇒a=0.225，
直径位于区间[110，112）的频数为100×2×0.050=10，位于区间[112，114）的频数为100×2×0.150=30，
位于区间[114，116）的频数为100×2×0.225=45，位于区间[116，118）的频数为100×2×0.075=15，
∴生产一件A产品的平均利润为

10×10+20×30+30×45+10×15

100

=22（元）；
（II）由频率分布直方图得：直径位于区间[112，114）和[114，116）的频率之比为2：3，
∴应从直径位于区间[112，114）的产品中抽取2件产品，记为A、B，
从直径位于区间[114，116）的产品中抽取3件产品，记为a、b、c，从中随机抽取两件，所有可能的取法有，（A，B），（A，a），（A，b），（A，c），（B，a），（B，b），（B，c）
，（a，b），（a，c），（b，c）10种，两件产品都不在区间[114，116）的取法只有（A，B）一种，
∴两件产品中至少有一件产品的直径位于区间[114，116）内的取法有9种．
∴所求概率为P=

9

10

．

点评：本题考查了分层抽样方法，考查了古典概型的概率计算，读懂频率分布直方图是解答本题的关键．