题目内容
已知函数f(x)=alnx-ax-3(a∈R),
(1)若函数y=f(x)在点(2,f(2))处的切线斜率为1,求a的值;
(2)在(1)的条件下,对任意t∈[1,2],函数g(x)=x3+x2[
+f′(x)]在区间(t,3)总存在极值,求m的取值范围;
(3)若a=2,对于函数h(x)=(p-2)x-
-3在[1,e]上至少存在一个x0使得h(x0)>f(x0)成立,求实数P的取值范围.
(1)若函数y=f(x)在点(2,f(2))处的切线斜率为1,求a的值;
(2)在(1)的条件下,对任意t∈[1,2],函数g(x)=x3+x2[
| m |
| 2 |
(3)若a=2,对于函数h(x)=(p-2)x-
| p+2e |
| x |
考点:导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(1)根据导数的几何意义,由题意即得f′(2)=-
=1,解得a=-2.
(2)根据函数极值的定义结合二次函数图象的特点,列出不等式求解即得结论;
(3)构造函数F(x)=h(x)-f(x)=px-
-2lnx,由题意得F(x)max=F(e)=pe-
-4,只要pe-
-4>0即可.
| a |
| 2 |
(2)根据函数极值的定义结合二次函数图象的特点,列出不等式求解即得结论;
(3)构造函数F(x)=h(x)-f(x)=px-
| p+2e |
| x |
| p |
| e |
| p |
| e |
解答:
解:(1)∵f(x)=alnx-ax-3(a∈R),
∴f′(x)=
-a,∵函数y=f(x)在点(2,f(2))处的切线斜率为1,
∴f′(2)=-
=1,解得a=-2.
(2)由(1)知,f(x)=-2lnx+2x-3,f′(x)=2-
,
∴g(x)=x3+(2+
)x2-2x,g′(x)=3x2+(m+4)x-2,
∵函数g(x)在区间(t,3)总存在极值,
∴
解得-
<m<-9.
(3)由a=2得f(x)=2lnx-2x-3,令F(x)=h(x)-f(x)=px-
-2lnx,则F′(x)=
,
①若p≤0,由于px-
≤0,-
-2lnx<0,故F(x)<0,所以不存在x0使得h(x0)>f(x0);
②若p>0,此时F′(x)=
>0,所以F(x)在[1,e]上是增函数,
∴F(x)max=F(e)=pe-
-4,只要pe-
-4>0即可,解得p>
,
即p∈(
,+∞).
∴f′(x)=
| a |
| x |
∴f′(2)=-
| a |
| 2 |
(2)由(1)知,f(x)=-2lnx+2x-3,f′(x)=2-
| 2 |
| x |
∴g(x)=x3+(2+
| m |
| 2 |
∵函数g(x)在区间(t,3)总存在极值,
∴
|
| 37 |
| 3 |
(3)由a=2得f(x)=2lnx-2x-3,令F(x)=h(x)-f(x)=px-
| p+2e |
| x |
| px2-2x+p+2e |
| x2 |
①若p≤0,由于px-
| p |
| x |
| 2e |
| x |
②若p>0,此时F′(x)=
| px2-2x+p+2e |
| x2 |
∴F(x)max=F(e)=pe-
| p |
| e |
| p |
| e |
| 4e |
| e2-1 |
即p∈(
| 4e |
| e2-1 |
点评:本题主要考查利用导数求曲线上过某点切线方程的斜率,会利用导数研究函数的极值及最值,掌握不等式成立时所取的条件,能够将其等价转化为求函数最值问题解决,逻辑能力强,属难题.

练习册系列答案
相关题目
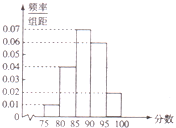 某校高三有800名同学参加学校组织的数学学科竞赛,其成绩的频率分布直方图如图所示,规定95分及其以上为一等奖.
某校高三有800名同学参加学校组织的数学学科竞赛,其成绩的频率分布直方图如图所示,规定95分及其以上为一等奖.