题目内容
已知函数f(x)=1-cosx(0<x<
).数列{an}满足:0<a1<
,an+1=f(an),n∈N*.
(Ⅰ)求证:0<an<
(n∈N*);
(Ⅱ)求证:数列{an}是递减数列.
| π |
| 2 |
| π |
| 2 |
(Ⅰ)求证:0<an<
| π |
| 2 |
(Ⅱ)求证:数列{an}是递减数列.
考点:数列递推式,数列的函数特性
专题:点列、递归数列与数学归纳法
分析:(Ⅰ)利用数学归纳法即可证明:0<an<
(n∈N*);
(Ⅱ)构造函数,利用导数研究函数的单调性,即可证明数列{an}是递减数列.
| π |
| 2 |
(Ⅱ)构造函数,利用导数研究函数的单调性,即可证明数列{an}是递减数列.
解答:
解:(Ⅰ)①当n=1时,显然成立,
②假设n=k时,0<ak<
,则cosak∈(0,1),
∴ak+1=1-cosak∈(0,1),
∴当n=k+1时,原不等式成立,
由①②可知0<an<
(n∈N*);
(Ⅱ)要证数列{an}是递减数列,即证an+1<an,
即证f(an)<an,
即1-cosan<an,
令g(x)=x+cosx-1,0<x<
,
g′(x)=1-sinx>0,
∴g(x)=x+cosx-1在0<x<
上单调递增,
∴当x>0时,g(x)>g(0)=0,
即x>1-cosx,0<x<
,
∴1-cosan<an,
即数列{an}是递减数列.
②假设n=k时,0<ak<
| π |
| 2 |
∴ak+1=1-cosak∈(0,1),
∴当n=k+1时,原不等式成立,
由①②可知0<an<
| π |
| 2 |
(Ⅱ)要证数列{an}是递减数列,即证an+1<an,
即证f(an)<an,
即1-cosan<an,
令g(x)=x+cosx-1,0<x<
| π |
| 2 |
g′(x)=1-sinx>0,
∴g(x)=x+cosx-1在0<x<
| π |
| 2 |
∴当x>0时,g(x)>g(0)=0,
即x>1-cosx,0<x<
| π |
| 2 |
∴1-cosan<an,
即数列{an}是递减数列.
点评:本题主要考查递推数列的应用,利用数学归纳法是解决不等式的基本方法,综合考查了函数单调性和导数之间的关系.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
在复平面内,复数
-i3对应的点位于( )
| 2 |
| 1-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
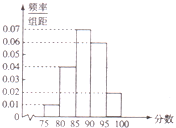 某校高三有800名同学参加学校组织的数学学科竞赛,其成绩的频率分布直方图如图所示,规定95分及其以上为一等奖.
某校高三有800名同学参加学校组织的数学学科竞赛,其成绩的频率分布直方图如图所示,规定95分及其以上为一等奖.