题目内容
已知函数f(x)=sinωx•cosωx+
cos2ωx-
(ω>0),直线x=x1,x=x2是y=f(x)图象的任意两条对称轴,且|x1-x2|的最小值为
.
(Ⅰ)求f(x)在x∈[-π,0]的单调增区间;
(Ⅱ)将函数f(x)的图象向右平移
个单位后,再将得到的图象上各点的横坐标伸长为原来的2倍,纵坐标不变,得到函数y=g(x)的图象,若关于x的方程g(x)+k=0,在区间[0,
]上有解,求实数k的取值范围.
| 3 |
| ||
| 2 |
| π |
| 4 |
(Ⅰ)求f(x)在x∈[-π,0]的单调增区间;
(Ⅱ)将函数f(x)的图象向右平移
| π |
| 8 |
| π |
| 2 |
考点:函数y=Asin(ωx+φ)的图象变换,三角函数中的恒等变换应用
专题:三角函数的图像与性质
分析:(Ⅰ)利用三角恒等变换可求得f(x)=sin(2ωx+
),依题意,可求得函数y=f(x)的最小正周期T=
=
,解得ω=2,从而可求得f(x)在x∈[-π,0]的单调增区间;
(Ⅱ)利用函数y=Asin(ωx+φ)的图象变换可求得g(x)=sin(2x-
),利用正弦函数的单调性可求得关于x的方程g(x)+k=0,在区间[0,
]上有解时,实数k的取值范围.
| π |
| 3 |
| 2π |
| 2ω |
| π |
| 2 |
(Ⅱ)利用函数y=Asin(ωx+φ)的图象变换可求得g(x)=sin(2x-
| π |
| 6 |
| π |
| 2 |
解答:
解:f(x)=sinωx•cosωx+
cos2ωx-
=
sin2ωx+
•
-
=
sin2ωx+
cos2ωx=sin(2ωx+
)…2分
(Ⅰ)∵直线x=x1,x=x2是y=f(x)图象的任意两条对称轴,且|x1-x2|的最小值为
.
∴函数y=f(x)的最小正周期T=
=
,∴ω=2…4分
∴f(x)=sin(4x+
)…5分
令2kπ-
≤4x+
≤2kπ+
,解得
-
≤x≤
+
(k∈Z),
∵x∈[-π,0],故该函数的单调增区间是[-π,-
π],[-
π,-
π],[-
,0],
…8分;
(Ⅱ)将函数f(x)的图象向右平移
个单位后得函数解析式为y=sin[4(x-
)+
]=sin(4x-
),
…9分
再将得到的图象上各点的横坐标伸长为原来的2倍,纵坐标不变,得到函数y=g(x)=sin(2x-
)的图象,
…10分
∵x∈[0,
],
∴g(x)=-k∈[-
,1],
∴k∈[-1,
]…12分
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 1+cos2ωx |
| 2 |
| ||
| 2 |
=
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
(Ⅰ)∵直线x=x1,x=x2是y=f(x)图象的任意两条对称轴,且|x1-x2|的最小值为
| π |
| 4 |
∴函数y=f(x)的最小正周期T=
| 2π |
| 2ω |
| π |
| 2 |
∴f(x)=sin(4x+
| π |
| 3 |
令2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| kπ |
| 2 |
| 5π |
| 24 |
| kπ |
| 2 |
| π |
| 24 |
∵x∈[-π,0],故该函数的单调增区间是[-π,-
| 23 |
| 24 |
| 17 |
| 24 |
| 11 |
| 24 |
| 5π |
| 24 |
…8分;
(Ⅱ)将函数f(x)的图象向右平移
| π |
| 8 |
| π |
| 8 |
| π |
| 3 |
| π |
| 6 |
…9分
再将得到的图象上各点的横坐标伸长为原来的2倍,纵坐标不变,得到函数y=g(x)=sin(2x-
| π |
| 6 |
…10分
∵x∈[0,
| π |
| 2 |
∴g(x)=-k∈[-
| 1 |
| 2 |
∴k∈[-1,
| 1 |
| 2 |
点评:本题考查三角恒等变换与函数y=Asin(ωx+φ)的图象变换,突出考查正弦函数的单调性、对称性、周期性及最值的综合应用,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在三棱椎P-ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC上的一点,它的正视图和侧视图如图所示,则下列命题正确的是( )
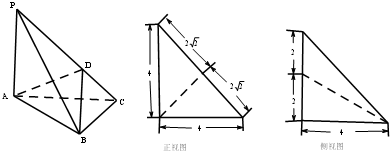

A、AD⊥平面PBC且三棱椎D-ABC的体积为
| ||
B、BD⊥平面PAC且三棱椎D-ABC的体积为
| ||
C、AD⊥平面PBC且三棱椎D-ABC的体积为
| ||
D、BD⊥平面PAC且三棱椎D-ABC的体积为
|