题目内容

已知A={x|log2x＜2}，B={x|
1
3
＜3x＜
3
}，则A∩B为（　　）
A、（0，
1
2
）
B、（0，
2
）
C、（-1，
1
2
）
D、（-1，
2
）
考点：交集及其运算
专题：集合
分析：求出A与B中不等式的解集确定出A与B，找出两集合的交集即可．
解答： 解：由A中的不等式变形得：log2x＜2=log24，解得：0＜x＜4}，即A=（0，4），
由B中不等式变形得：3-1=
1
3
＜3x＜
3
=3
1
2
，解得：-1＜x＜
1
2
，即B=（-1，
1
2
），
则A∩B=（0，
1
2
）．
故选：A．
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目
已知函数f（x）（x∈R）的图象上任一点（x0，y0）处切线的方程为：y-y0=（x0-2）（ x0-1）（x-x0），那么函数f（x）的单调减区间是（　　）
A、（1，2）
B、（-∞，1]
C、[2，+∞）
D、（-∞，-1）
在复平面内，复数
2
1-i
-i3对应的点位于（　　）
A、第一象限B、第二象限
C、第三象限D、第四象限
已知函数f（x）=ax2+bx+c（a，b，c∈R，a＜0）对于一切实数x都有f（1-x）=f（1+x），而且f（-1）＜0，f（0）＞0，则有（　　）
A、a+b+c＜0
B、c＜2b
C、abc＞0
D、b＜a+c
已知
1
2
sin（π-2x）-1=cos2x（0＜x＜π），则tan2x的值是（　　）
A、-
4
3
B、
4
3
C、-
2
3
D、
2
3
在三棱椎P-ABC中，PA⊥平面ABC，AC⊥BC，D为侧棱PC上的一点，它的正视图和侧视图如图所示，则下列命题正确的是（　　）
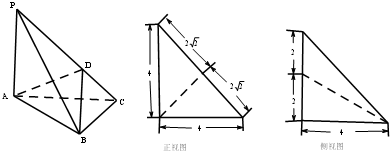
A、AD⊥平面PBC且三棱椎D-ABC的体积为
8
3
B、BD⊥平面PAC且三棱椎D-ABC的体积为
8
3
C、AD⊥平面PBC且三棱椎D-ABC的体积为
16
3
D、BD⊥平面PAC且三棱椎D-ABC的体积为
16
3
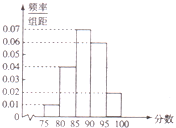某校高三有800名同学参加学校组织的数学学科竞赛，其成绩的频率分布直方图如图所示，规定95分及其以上为一等奖．
区间 [75，80） [80，85） [85，90） [90，95） [95，100]
人数 40 a 280 240 b
（Ⅰ）上表是这次考试成绩的频数分布表，求正整数a，b的值；
（Ⅱ）现在要用分层抽样的方法从这800人中抽取40人的成绩进行分析，求其中获二等奖的学生人数；
（Ⅲ）在（Ⅱ）中抽取的40名学生中，要随机选取2名学生参加市全省数学学科竞赛，记“其中一等奖的人数”为X，求X的分布列与数学期望．
数列{an}满足a1=t，an+1=
tan
an+1
，其中t＞0．
（Ⅰ）当t=1时，求证数列{
1
an
}是等差数列；
（Ⅱ）当t≠1时，求证数列{
1
an
-
1
t-1
}是等比数列，并求出数列{an}的通项公式；
（Ⅲ）试证明：对于一切正整数n，不等式2nan≤tn+1+1均成立．
已知函数r（x）=lnx，函数h（x）=
1
a
(1-
1
x
)(a＞0)，f(x)=r(x)-h(x)．
（Ⅰ）试求f（x）的单调区间．
（Ⅱ）若f（x）在区间[1，+∞）上是单调递增函数，试求实数a的取值范围：
（Ⅲ）设数列{an}是公差为1．首项为l的等差数列，数列{
1
an
}的前n项和为Sn，求证：当a=1时，Sn-2＜f（n）-
1
n
＜Sn-1-1(n∈N*，n≥2)．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网