题目内容
正三棱柱ABC-A1B1C1的底面边长为3,侧棱AA1=
,D是CB延长线上一点,且BD=BC,则二面角B1-AD-B的大小( )
| 3 |
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:二面角的平面角及求法
专题:空间位置关系与距离
分析:过B作BE⊥AD于E,连接EB1,根据三垂线定理得∠B1EB是二面角B1-AD-B的平面角,在Rt△BB1E中,利用三角函数的定义可算出∠B1EB=
,即二面角B1-AD-B的大小为
.
| π |
| 3 |
| π |
| 3 |
解答:
解:过B作BE⊥AD于E,连接EB1,
∵BB1⊥平面ABD,∴BE是B1E在平面ABD内的射影,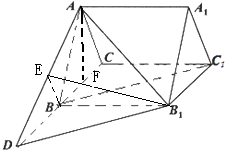
结合BE⊥AD,可得B1E⊥AD,
∴∠B1EB是二面角B1-AD-B的平面角,
∵BD=BC=AB,
∴E是AD的中点,得BE是三角形ACD的中位线,所以BE=
AC=
,
在Rt△BB1E中,tan∠B1BE=
=
=
,
∴∠B1EB=
,即二面角B1-AD-B的大小为
,
故选:A.
∵BB1⊥平面ABD,∴BE是B1E在平面ABD内的射影,

结合BE⊥AD,可得B1E⊥AD,
∴∠B1EB是二面角B1-AD-B的平面角,
∵BD=BC=AB,
∴E是AD的中点,得BE是三角形ACD的中位线,所以BE=
| 1 |
| 2 |
| 3 |
| 2 |
在Rt△BB1E中,tan∠B1BE=
| B1B |
| BE |
| ||||
|
| 3 |
∴∠B1EB=
| π |
| 3 |
| π |
| 3 |
故选:A.
点评:本题以一个特殊正三棱柱为载体,适当加以变化,求三棱锥的二面角的大小,着重考查了空间线面面面垂直的判定与性质等知识点,属于中档题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目