题目内容
设数列{an}的前n项和为Sn,若对任意n∈N*,都有Sn=3an-5n.
(1)求数列{an}的首项;
(2)若数列{an+λ}是等比数列,试求出实数λ的值,并写出数列{an}的通项公式;
(3)数列{bn}满足bn=
,是否存在m,对任意n∈N*使得bn≤bm成立?如果存在,求出正整数m的值,如果不存在,说明理由.
(1)求数列{an}的首项;
(2)若数列{an+λ}是等比数列,试求出实数λ的值,并写出数列{an}的通项公式;
(3)数列{bn}满足bn=
| 9n+4 |
| an+5 |
考点:数列与不等式的综合,等比数列的性质
专题:等差数列与等比数列,不等式的解法及应用
分析:(1)直接在数列递推式中取n=1求得数列首项;
(2)在数列递推式中取n=n-1得另一递推式,作差后得到{an+5}是以
为公比的等比数列,即λ的值是5.然后由等比数列的通项公式求得数列{an}的通项公式;
(3)把数列{an}的通项公式代入足bn=
,利用作商法得到当n≥3时,
<1,当n=2时,
>1,由此可得答案.
(2)在数列递推式中取n=n-1得另一递推式,作差后得到{an+5}是以
| 3 |
| 2 |
(3)把数列{an}的通项公式代入足bn=
| 9n+4 |
| an+5 |
| bn |
| bn-1 |
| bn |
| bn-1 |
解答:
解:(1)∵Sn=3an-5n ①,
∴S1=a1=3a1-5,解得a1=
;
(2)由Sn=3an-5n,得Sn-1=3an-1-5(n-1),n≥2 ②.
①-②得,an=
an-1+
,
∴an+5=
(an-1+5),
∴{an+5}是以
为公比的等比数列,即λ的值是5.
∴an=
•(
)n-1-5;
(3)∵bn=
,
∴bn=
.
∴
=
=
.
-1=
=
.
∴当n≥3时,
<1,当n=2时,
>1,
∴当n=2时,bn有最大值b2=
.
∴m=2.
∴S1=a1=3a1-5,解得a1=
| 5 |
| 2 |
(2)由Sn=3an-5n,得Sn-1=3an-1-5(n-1),n≥2 ②.
①-②得,an=
| 3 |
| 2 |
| 5 |
| 2 |
∴an+5=
| 3 |
| 2 |
∴{an+5}是以
| 3 |
| 2 |
∴an=
| 15 |
| 2 |
| 3 |
| 2 |
(3)∵bn=
| 9n+4 |
| an+5 |
∴bn=
| 9n+4 | ||||
|
∴
| bn |
| bn-1 |
| ||||||
|
| 18n+8 |
| 27n-15 |
| 18n+8 |
| 27n-15 |
| 18n+8-27n+15 |
| 27n-15 |
| -9n+23 |
| 27n-15 |
∴当n≥3时,
| bn |
| bn-1 |
| bn |
| bn-1 |
∴当n=2时,bn有最大值b2=
| 264 |
| 135 |
∴m=2.
点评:本题考查了等比数列的通项公式,考查了利用作商法判断数列的单调性,考查了数列的函数特性,训练了利用单调性求函数的最值,是压轴题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
下列哪一组函数相等( )
A、f(x)=x与g(x)=
| |||
B、f(x)=x2与g(x)=(
| |||
C、f(x)=|x|与g(x)=(
| |||
D、f(x)=x2与g(x)=
|
若四面体的各棱长是1或2,且该四面体不是正四面体,则其体积不可能是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f(x)=
-
,(a∈R且a>0).
(1)判断函数f(x)的单调性,并证明;
(2)若函数f(x)的定义域为(-2,2)时,求使f(1-m)-f(m2-1)<0成立的实数m的取值范围.
| ex |
| a |
| a |
| ex |
(1)判断函数f(x)的单调性,并证明;
(2)若函数f(x)的定义域为(-2,2)时,求使f(1-m)-f(m2-1)<0成立的实数m的取值范围.
如图为一个四棱锥的正视图、侧(左)视图和俯视图,则该四棱锥的表面积为( )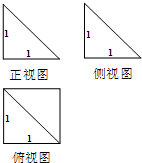

| A、3 | ||
B、2+
| ||
| C、2 | ||
D、3+2
|