题目内容
将2.1
，2.2
，0.3
这三个数从小到大排列为 ．
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
考点：不等式比较大小
专题：函数的性质及应用
分析：考察函数y=x
在R上单调递增，及指数函数的单调性，即可得出．
| 1 |
| 3 |
解答：
解：考察函数y=x
在R上单调递增，
∴1＜2．1
＜2．2
，
又0．3
＜1，
∴0．3
＜2．1
＜2．2
，
故答案为：0．3
＜2．1
＜2．2
．
| 1 |
| 3 |
∴1＜2．1
| 1 |
| 3 |
| 1 |
| 3 |
又0．3
| 1 |
| 2 |
∴0．3
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
故答案为：0．3
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
点评：本题考查了指数函数与幂函数的单调性，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=cos
x，f（x）=a在区间（
，2π）上恰有三个不同的实数根，且三个实数根从小到大依次成等比数列，则这三个实数根之和为（ ）
| 3 |
| 2 |
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若f（x）=（m-1）x2+2mx+3为偶函数，则f（x）在区间（-7，-2）上是（ ）
| A、减函数 | B、先减后增函数 |
| C、增函数 | D、先增后减函数 |
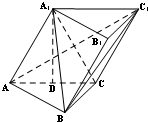如图所示，已知三棱柱ABC-A1B1C1，点A1在底面ABC上的射影恰为AC的中点D，∠BCA=90°，AC=BC=2，BA1⊥AC1．