题目内容
已知函数f(x)=cos
x,f(x)=a在区间(
,2π)上恰有三个不同的实数根,且三个实数根从小到大依次成等比数列,则这三个实数根之和为( )
| 3 |
| 2 |
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:余弦函数的图象
专题:等差数列与等比数列,三角函数的图像与性质
分析:作出函数y=cos
x的图象和直线y=a,得两个图象在(
,2π)上有三个交点A、B、C,满足A、B关于x=
对称且B、C关于x=
对称,结合三个根从小到大依次成等比数列列出横坐标x1、x2、x3的方程组,解之可得x2的值,从而,x1=
,x2=
,x3=
,得三个实数根之和为
.
| 3 |
| 2 |
| π |
| 3 |
| 2π |
| 3 |
| 4π |
| 3 |
| 4π |
| 9 |
| 8π |
| 9 |
| 16π |
| 9 |
| 28π |
| 9 |
解答:
解:同一坐标系中作出y=cosx和y=a的图象,
设两个图象在(
,2π)上有三个交点A、B、C,则A、B、C的
横坐标分别对应方程f(x)=a的三个根,
得A(x1,a),B(x2,a),A(x3,a),
根据余弦函数图象的对称性,得
=
,得x1+x2=
且
=
,x2+x3=
∵三个根从小到大依次成等比数列,即x22=x1x3,
∴x22=(
-x2)(
-x2),解之得x2=
,
因此,x1=
,x2=
,x3=
,得三个实数根之和为
.
故选:D.

设两个图象在(
| π |
| 3 |
横坐标分别对应方程f(x)=a的三个根,
得A(x1,a),B(x2,a),A(x3,a),
根据余弦函数图象的对称性,得
| x1+x2 |
| 2 |
| 2π |
| 3 |
| 4π |
| 3 |
且
| x2+x3 |
| 2 |
| 4π |
| 3 |
| 8π |
| 3 |
∵三个根从小到大依次成等比数列,即x22=x1x3,
∴x22=(
| 4π |
| 3 |
| 8π |
| 3 |
| 8π |
| 9 |
因此,x1=
| 4π |
| 9 |
| 8π |
| 9 |
| 16π |
| 9 |
| 28π |
| 9 |
故选:D.

点评:本题给出余弦曲线上三个点构成两组对称的点,着重考查了等比数列的性质和余弦函数的图象与性质等知识,属于中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
若从1,2,3,4,5,6,7,8,9,10这10个数中任意取出3个数,则这三个数互不相邻的取法种数有( )
| A、20种 | B、56种 |
| C、60种 | D、120种 |
若复数z与(z-1)2-2i都是纯虚数,则z=( )
| A、i | B、-i | C、±i | D、1 |
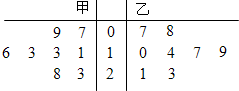 某篮球队甲、乙两名队员在本赛季已结束的8场比赛中得分统计的茎叶图如图:若以甲、乙两名队员得分的频率作为概率,假设甲、乙两名队员在同一场比赛中的得分互不影响.
某篮球队甲、乙两名队员在本赛季已结束的8场比赛中得分统计的茎叶图如图:若以甲、乙两名队员得分的频率作为概率,假设甲、乙两名队员在同一场比赛中的得分互不影响. 已知函数f(x)=ax+b(a>0,a≠1)的图象如图所示,则a-b的值为
已知函数f(x)=ax+b(a>0,a≠1)的图象如图所示,则a-b的值为