题目内容
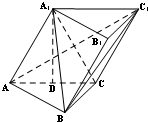 如图所示,已知三棱柱ABC-A1B1C1,点A1在底面ABC上的射影恰为AC的中点D,∠BCA=90°,AC=BC=2,BA1⊥AC1.
如图所示,已知三棱柱ABC-A1B1C1,点A1在底面ABC上的射影恰为AC的中点D,∠BCA=90°,AC=BC=2,BA1⊥AC1.(Ⅰ)求证:AC1⊥平面A1BC;
(Ⅱ)求二面角B1-A1B-C1的余弦值.
考点:用空间向量求平面间的夹角,直线与平面垂直的判定
专题:空间位置关系与距离,空间角,空间向量及应用
分析:(Ⅰ)取AB中点E,连接DE,容易证明DE,DC,DA1三条直线两两垂直,所以分别以这三条直线为x,y,z轴建立空间直角坐标系,设DA1=t,根据告诉的边的长度和边的关系求出点A,B,C,A1,C1的坐标,从而求出
,
的坐标,从而能求出
•
=0,所以得出AC1⊥BC,再根据已知的AC1⊥BA1,即可得出AC1⊥平面A1BC;
(Ⅱ)根据两平面所成二面角与这两个平面法向量夹角的关系:相等或互补,所以求平面A1BB1,和平面A1BC1的法向量,设平面A1BB1的法向量为
=(x,y,z),则
⊥
,
⊥
,根据垂直数量积为0即可求出该平面的一个法向量,同样的方法求出平面A1BC1的一个法向量,然后求这两个法向量夹角的余弦值即可.
| AC1 |
| BC |
| AC1 |
| BC |
(Ⅱ)根据两平面所成二面角与这两个平面法向量夹角的关系:相等或互补,所以求平面A1BB1,和平面A1BC1的法向量,设平面A1BB1的法向量为
| m |
| m |
| A1B |
| m |
| BB1 |
解答:
解:如图所示,取AB的中点E,连接DE,则DE∥BC,∵BC⊥AC,∴DE⊥AC;

又A1D⊥平面ABC,以D为原点建立如图所示的空间直角坐标系;
设DA1=t,(t>0),则A(0,-1,0),B(2,1,0),C(0,1,0),A1(0,0,t),C1(0,2,t);
(Ⅰ)证明:
=(0,3,t),
=(-2,-1,t),
=(-2,0,0);
∴
•
=0,∴
⊥
,∴AC1⊥CB,又AC1⊥BA1,∴AC1⊥平面A1BC;
(Ⅱ)因为
=(-2,-1,t),
=(0,3,t),由BA1⊥AC1得t2=3,∴t=
;
∴
=(-2,-1,
),
=
=(0,1,
),
=(0,2,0);
设平面A1BB1的一个法向量为
=(x,y,z),则
,∴x=
z,y=-
z,∴可取
=(
,-
,1);同理:
可求得平面A1BC1的一个法向量为
=(
,0,2),∴cos<
,
>=
=
;
所以,二面角B1-A1B-C1的余弦值为
.

又A1D⊥平面ABC,以D为原点建立如图所示的空间直角坐标系;
设DA1=t,(t>0),则A(0,-1,0),B(2,1,0),C(0,1,0),A1(0,0,t),C1(0,2,t);
(Ⅰ)证明:
| AC1 |
| BA1 |
| BC |
∴
| AC1 |
| BC |
| AC1 |
| BC |
(Ⅱ)因为
| BA1 |
| AC1 |
| 3 |
∴
| BA1 |
| 3 |
| BB1 |
| AA1 |
| 3 |
| A1C1 |
设平面A1BB1的一个法向量为
| m |
|
| 3 |
| 3 |
| m |
| 3 |
| 3 |
可求得平面A1BC1的一个法向量为
| n |
| 3 |
| m |
| n |
| ||||
|
|
| 5 |
| 7 |
所以,二面角B1-A1B-C1的余弦值为
| 5 |
| 7 |
点评:考查通过建立空间直角坐标系,用向量解决立体几何问题的方法,两向量数量积为0的充要条件,线面垂直的判定定理,向量夹角的余弦公式,平面的法向量的概念.

练习册系列答案
相关题目
若复数z与(z-1)2-2i都是纯虚数,则z=( )
| A、i | B、-i | C、±i | D、1 |
下列命题中是假命题的是( )
A、?x∈(0,
| ||
| B、?x0∈R,sinx0+cosx0=2 | ||
| C、?x∈R,3x>0 | ||
| D、?x0∈R,lgx0=0 |
已知奇函数f(x)在(-∞,0)上单调递增,且f(2)=0,则不等式(x-1)•f(x-1)>0的解集是( )
| A、(-1,3) |
| B、(-∞-1) |
| C、(-∞-1)∪(3,+∞) |
| D、(-1,1)∪(1,3) |
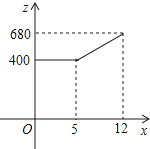 我市某服装厂生产的服装供不应求,A车间接到生产一批西服的紧急任务,要求必须在12天内完成.为了加快进度,车间采取工人分批日夜加班,机器满负荷运转的生产方式,生产效率得到了提高,每天生产的西服数量y(套)与时间x(天)的关系如下表:
我市某服装厂生产的服装供不应求,A车间接到生产一批西服的紧急任务,要求必须在12天内完成.为了加快进度,车间采取工人分批日夜加班,机器满负荷运转的生产方式,生产效率得到了提高,每天生产的西服数量y(套)与时间x(天)的关系如下表: