题目内容
已知函数f(x)=
(其中a>0且a≠1).
(1)求函数f(x)的值域;
(2)判断奇偶性并证明之;
(3)判断单调性并证明之.
| ax-a-x |
| ax+a-x |
(1)求函数f(x)的值域;
(2)判断奇偶性并证明之;
(3)判断单调性并证明之.
考点:函数奇偶性的判断,函数的值域,函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)首先对函数关系是进行恒等变换转换成f(x)=1-
,进一步利用指数函数的值域确定该函数的值域.
(2)利用定义判断函数的奇偶性①定义域的对称问题②f(-x)与f(x)的关系.
(3)采用分类讨论思想①0<a<1①0<a<1进一步利用单调性进行证明.
| 2 |
| a2x+1 |
(2)利用定义判断函数的奇偶性①定义域的对称问题②f(-x)与f(x)的关系.
(3)采用分类讨论思想①0<a<1①0<a<1进一步利用单调性进行证明.
解答:
解:(1)已知函数f(x)=
(a>0且a≠1)
则:f(x)=
=
=1-
由于a>0且a≠1
则:a2x>0
进一步求得:0<
<2
所以:1>f(x)>-1
即:函数f(x)的值域:(-1,1)
(2)函数f(x)是奇函数.
证明:①x∈R
②f(-x)=
=-f(x),
所以函数f(x)是奇函数;
(3)函数f(x)①0<a<1为减函数②a>1为增函数.
证明:由(1)得f(x)=1-
(a>0且a≠1),
①0<a<1,
a2x在定义域x∈R内为单调递减函数,
则:
为单调递增函数,
进一步求得f(x)=1-
在定义域x∈R内为单调递减函数;
②a>1,
a2x在定义域x∈R内为单调递增函数
则:
为单调递减函数
进一步求得f(x)=1-
在定义域x∈R内为单调递增函数
故答案为:(1)函数f(x)的值域:(-1,1)
(2)函数f(x)是奇函数
(3)函数f(x)①0<a<1为减函数②a>1为增函数
| ax-a-x |
| ax+a-x |
则:f(x)=
ax-
| ||
ax+
|
| a2x-1 |
| a2x+1 |
| 2 |
| a2x+1 |
由于a>0且a≠1
则:a2x>0
进一步求得:0<
| 2 |
| a2x+1 |
所以:1>f(x)>-1
即:函数f(x)的值域:(-1,1)
(2)函数f(x)是奇函数.
证明:①x∈R
②f(-x)=
| a-x-ax |
| ax+a-x |
所以函数f(x)是奇函数;
(3)函数f(x)①0<a<1为减函数②a>1为增函数.
证明:由(1)得f(x)=1-
| 2 |
| a2x+1 |
①0<a<1,
a2x在定义域x∈R内为单调递减函数,
则:
| 2 |
| a2x+1 |
进一步求得f(x)=1-
| 2 |
| a2x+1 |
②a>1,
a2x在定义域x∈R内为单调递增函数
则:
| 2 |
| a2x+1 |
进一步求得f(x)=1-
| 2 |
| a2x+1 |
故答案为:(1)函数f(x)的值域:(-1,1)
(2)函数f(x)是奇函数
(3)函数f(x)①0<a<1为减函数②a>1为增函数
点评:本题考查的知识要点:函数的恒等变换.求函数的值域,判断函数的奇偶性的两个条件,利用指数函数的单调性判断函数的单调性分类讨论思想在题中的应用.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
若复数z与(z-1)2-2i都是纯虚数,则z=( )
| A、i | B、-i | C、±i | D、1 |
 已知函数f(x)=ax+b(a>0,a≠1)的图象如图所示,则a-b的值为
已知函数f(x)=ax+b(a>0,a≠1)的图象如图所示,则a-b的值为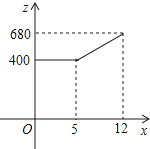 我市某服装厂生产的服装供不应求,A车间接到生产一批西服的紧急任务,要求必须在12天内完成.为了加快进度,车间采取工人分批日夜加班,机器满负荷运转的生产方式,生产效率得到了提高,每天生产的西服数量y(套)与时间x(天)的关系如下表:
我市某服装厂生产的服装供不应求,A车间接到生产一批西服的紧急任务,要求必须在12天内完成.为了加快进度,车间采取工人分批日夜加班,机器满负荷运转的生产方式,生产效率得到了提高,每天生产的西服数量y(套)与时间x(天)的关系如下表: