题目内容
设an(n=2,3,4,…)是(2+x)n的展开式中x2项的系数,则
×(
+
+
+…+
)=( )
| 2010 |
| 2009 |
| 22 |
| a2 |
| 23 |
| a3 |
| 24 |
| a4 |
| 22010 |
| a2010 |
| A、8 | B、4 | C、2 | D、1 |
考点:二项式定理的应用
专题:二项式定理
分析:由题意求得an,可得
=8(
-
),故要求的式子即
×8×[(1-
)+(
-
)+(
-
)+…+(
-
)],计算求得结果.
| 2n |
| an |
| 1 |
| n-1 |
| 1 |
| n |
| 2010 |
| 2009 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2009 |
| 1 |
| 2010 |
解答:
解:由题意可得an=
•2n-2=n(n-1)•2n-3,∴
=
=8(
-
),
则
×(
+
+
+…+
)=
×8[(1-
)+(
-
)+(
-
)+…+(
-
)]
=
×8×(1-
)=8,
故选:A.
| C | 2 n |
| 2n |
| an |
| 8 |
| n(n-1) |
| 1 |
| n-1 |
| 1 |
| n |
则
| 2010 |
| 2009 |
| 22 |
| a2 |
| 23 |
| a3 |
| 24 |
| a4 |
| 22010 |
| a2010 |
| 2010 |
| 2009 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2009 |
| 1 |
| 2010 |
=
| 2010 |
| 2009 |
| 1 |
| 2010 |
故选:A.
点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,用裂项法进行数列求和,属于基础题.

练习册系列答案
相关题目
若2014a=
,2014b=3,则a+2b等于( )
| 2014 |
| 9 |
| A、0 | B、1 | C、2 | D、3 |
设函数f(x)(x∈R)满足f(-x)=f(x),f(x)=f(2-x),且当x∈[0,1]时,f(x)=x3,又函数g(x)=|cos(πx)|,则函数h(x)=g(x)-f(x)在[-
,
]上的零点个数为( )
| 1 |
| 2 |
| 3 |
| 2 |
| A、8 | B、7 | C、6 | D、5 |
若从1,2,3,4,5,6,7,8,9,10这10个数中任意取出3个数,则这三个数互不相邻的取法种数有( )
| A、20种 | B、56种 |
| C、60种 | D、120种 |
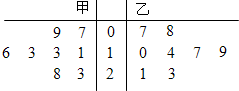 某篮球队甲、乙两名队员在本赛季已结束的8场比赛中得分统计的茎叶图如图:若以甲、乙两名队员得分的频率作为概率,假设甲、乙两名队员在同一场比赛中的得分互不影响.
某篮球队甲、乙两名队员在本赛季已结束的8场比赛中得分统计的茎叶图如图:若以甲、乙两名队员得分的频率作为概率,假设甲、乙两名队员在同一场比赛中的得分互不影响. 已知函数f(x)=ax+b(a>0,a≠1)的图象如图所示,则a-b的值为
已知函数f(x)=ax+b(a>0,a≠1)的图象如图所示,则a-b的值为