题目内容
若4a2+3b2=4,求y=(2a2+1)•(b2+2)的最大值.
考点:基本不等式
专题:不等式的解法及应用
分析:本题利用已知的和为定值,将要求的积中两数转化为和是定值的情况,用基本不等式法,得到积的最大值.
解答:
解:利用基本不等式,有:当x>0,y>0时,有xy≤(
)2.
∵4a2+3b2=4,
∴y=(2a2+1)•(b2+2)
=
(4a2+2)(3b2+6)
≤
[
]2
=
(
)2
=
×(
)2
=6
当且仅当4a2+2=3b2+6,即a2=1,b2=0时,不等式取最值.
∴y=(2a2+1)•(b2+2)的最大值为6.
| x+y |
| 2 |
∵4a2+3b2=4,
∴y=(2a2+1)•(b2+2)
=
| 1 |
| 6 |
≤
| 1 |
| 6 |
| (4a2+2)+(3b2+6) |
| 2 |
=
| 1 |
| 6 |
| 4a2+3b2+8 |
| 2 |
=
| 1 |
| 6 |
| 4+8 |
| 2 |
=6
当且仅当4a2+2=3b2+6,即a2=1,b2=0时,不等式取最值.
∴y=(2a2+1)•(b2+2)的最大值为6.
点评:本题考查的是基本不等式,注意不等式使用的条件“一正、二定、三相等”,要配凑成和为定值的形式,并关注取等号的条件.本题有一定难度,但运算量不大,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知f1(x)=sinx+cosx,fn+1(x)是fn(x)的导函数,即f2(x)=f1′(x),f3(x)=f2′(x),…,fn+1(x)=fn′(x),n∈N*,则f2014(x)等于( )
| A、-sinx-cosx |
| B、sinx-cosx |
| C、sinx+cosx |
| D、-sinx+cosx |
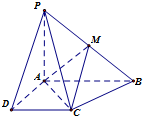 已知四棱锥P-ABCD的底面为直角梯形,AB∥CD,∠DAB=
已知四棱锥P-ABCD的底面为直角梯形,AB∥CD,∠DAB=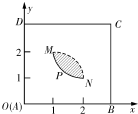 如图,矩形ABCD是一个观光区的平面示意图,建立平面直角坐标系,使顶点A在坐标原点O,B,D分别在x轴,y轴上,AD=3百米,AB=a百米(3≤a≤4)观光区中间叶形阴影部分MN是一个人工湖,它的左下方边缘曲线是函数y=
如图,矩形ABCD是一个观光区的平面示意图,建立平面直角坐标系,使顶点A在坐标原点O,B,D分别在x轴,y轴上,AD=3百米,AB=a百米(3≤a≤4)观光区中间叶形阴影部分MN是一个人工湖,它的左下方边缘曲线是函数y=