题目内容
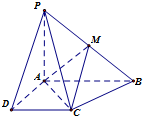 已知四棱锥P-ABCD的底面为直角梯形,AB∥CD,∠DAB=
已知四棱锥P-ABCD的底面为直角梯形,AB∥CD,∠DAB=| π |
| 2 |
| 1 |
| 2 |
(1)求证:直线CM∥平面PAD;
(2)若直线CM与平面ABCD所成的角为
| π |
| 4 |
考点:与二面角有关的立体几何综合题,直线与平面平行的判定
专题:空间角
分析:(1)取AB的中点N,由已知条件推导出MN∥平面PAD,CE∥平面PAD,从而得到平面CMN∥平面PAD,由此能证明CM∥平面PAD.
(2)由已知条件推导出CM与平面ABCD所成的角为∠MCN=
,△AMC和△BMC都是边长为
的正三角形,取CM的中点G,则∠AGB为二面角A-MC-B的平面角,由此能求出二面角A-MC-B的余弦值.
(2)由已知条件推导出CM与平面ABCD所成的角为∠MCN=
| π |
| 4 |
| 2 |
解答:
(1)证明:取AB的中点N,
则MN
PA,∴MN∥平面PAD,
又四边形ADCM正方形,∴CM
AD,∴CE∥平面PAD,
∴平面CMN∥平面PAD,
∴CM∥平面PAD.(4分)
(2)解:由PA⊥底面ABCD,得MN⊥底面ABCD,
则CM与平面ABCD所成的角为∠MCN=
,
∴PA=2MN=2CN=2AD=2,
∴△AMC和△BMC都是边长为
的正三角形,
取CM的中点G,则AG⊥CM,且BG⊥CM,(7分)
∴∠AGB为二面角A-MC-B的平面角,(9分)
在△AGB中,AG=BG=
,AB=2,
∴cos∠AGB=
=-
.
∴二面角A-MC-B的余弦值为-
.(12分)
则MN
| ∥ |
. |
| 1 |
| 2 |
又四边形ADCM正方形,∴CM
| ∥ |
. |

∴平面CMN∥平面PAD,
∴CM∥平面PAD.(4分)
(2)解:由PA⊥底面ABCD,得MN⊥底面ABCD,
则CM与平面ABCD所成的角为∠MCN=
| π |
| 4 |
∴PA=2MN=2CN=2AD=2,
∴△AMC和△BMC都是边长为
| 2 |
取CM的中点G,则AG⊥CM,且BG⊥CM,(7分)

∴∠AGB为二面角A-MC-B的平面角,(9分)
在△AGB中,AG=BG=
| ||
| 2 |
∴cos∠AGB=
| AG2+BG2-AB2 |
| 2AG•BG |
| 1 |
| 3 |
∴二面角A-MC-B的余弦值为-
| 1 |
| 3 |
点评:本题考查直线与平面平行的证明,考查二面角的余弦值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
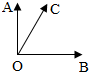 如图所示:|
如图所示:|| OA |
| OB |
| 3 |
| OA |
| OB |
| π |
| 6 |
| OC |
| OA |
| OB |
| λ |
| μ |
A、
| ||||
B、
| ||||
| C、3 | ||||
D、
|

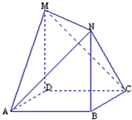 四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1.
四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1.