题目内容
已知f1（x）=sinx+cosx，fn+1（x）是fn（x）的导函数，即f2（x）=f1′（x），f3（x）=f2′（x），…，fn+1（x）=fn′（x），n∈N*，则f2014（x）等于（ ）
| A、-sinx-cosx |
| B、sinx-cosx |
| C、sinx+cosx |
| D、-sinx+cosx |
考点：导数的运算
专题：导数的概念及应用
分析：利用导数公式，分别求出函数的表达式，寻找出函数导数的规律即可．
解答：
解：∵f1（x）=sinx+cosx，
∴f2（x）=f′1（x）=cosx-sinx，
f3（x）=f′2（x）=-sinx-cosx，
f4（x）=f′3（x）=-cosx+sinx，
f5（x）=f′4（x）=sinx+cosx，
…，
即导函数是以4为周期的函数．
∴f2014（x）=f2（x）=cosx-sinx．
故选：D
∴f2（x）=f′1（x）=cosx-sinx，
f3（x）=f′2（x）=-sinx-cosx，
f4（x）=f′3（x）=-cosx+sinx，
f5（x）=f′4（x）=sinx+cosx，
…，
即导函数是以4为周期的函数．
∴f2014（x）=f2（x）=cosx-sinx．
故选：D
点评：本题主要考查了导数的基本运算，利用函数的导数值确定函数的周期性是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
已知复数z满足
=i（其中i是虚数单位），则z为（ ）
| z+2 |
| z-2 |
| A、2i | B、-2i | C、i | D、-i |
圆C1：x2+y2=1与圆C2：（x-2）2+y2=1的位置关系是（ ）
| A、相离 | B、相交 | C、内切 | D、外切 |
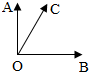如图所示：|| OA |
| OB |
| 3 |
| OA |
| OB |
| π |
| 6 |
| OC |
| OA |
| OB |
| λ |
| μ |
A、
| ||||
B、
| ||||
| C、3 | ||||
D、
|
某学校高一、高二、高三年级的学生人数分别为600，400，800．为了了解教师的教学情况，该校采用分层抽样的方法从这三个年级中抽取45名学生进行座谈，则高一、高二、高三年级抽取的人数分别为（ ）
| A、15，5，25 |
| B、15，15，15 |
| C、10，5，30 |
| D、15，10，20 |
