题目内容
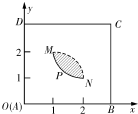 如图,矩形ABCD是一个观光区的平面示意图,建立平面直角坐标系,使顶点A在坐标原点O,B,D分别在x轴,y轴上,AD=3百米,AB=a百米(3≤a≤4)观光区中间叶形阴影部分MN是一个人工湖,它的左下方边缘曲线是函数y=
如图,矩形ABCD是一个观光区的平面示意图,建立平面直角坐标系,使顶点A在坐标原点O,B,D分别在x轴,y轴上,AD=3百米,AB=a百米(3≤a≤4)观光区中间叶形阴影部分MN是一个人工湖,它的左下方边缘曲线是函数y=| 2 |
| x |
(1)求花圃面积f(t)的表达式;
(2)求f(t)的最小值.
考点:导数在最大值、最小值问题中的应用,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)由导函数得到切线的斜率,通过切线的方程研究切线与x轴、y轴的交点坐标,根据交点位置确定图形的形态,得到所求的函数;
(2)对(1)所求得的分段函数进行分段研究,分别用配方法的求导法求出保段上的最小值,再比较它们的大小,从而得到函数的最小值.
(2)对(1)所求得的分段函数进行分段研究,分别用配方法的求导法求出保段上的最小值,再比较它们的大小,从而得到函数的最小值.
解答:
解:(1)由题意可知P(t,
),y′=-
,故过点P的切线方程为y-
=-
(x-t),
即y=-
x+
(1≤t≤2).切线l与x轴的交点为(2t,0),与y轴交点为(0,
).
①当
,即
≤t≤
时,切线左下方区域为直角三角形,
∴f(t)=
×2t×
=4;
②当
,即
<t≤2时,切线左下方区域为直角梯形,
∴f(t)=
(
+
)a=
;
③当
,即1≤t<
时,切线左下方区域为三角梯形,
f(t)=
(
+2t)•3=6t-
t2.
综上,f(t)=
.
(2)当1≤t<
时,f(t)=6t-
t2=-
(t-
)2+4,当t=1时,[f(t)]min=
<4;
当
<t≤2时,f(t)=
,f ′(t)=
<0,
∴f(t)在(
,2]上单调递减,[f(t)]min=f(2)=2a-
<4;
下面比较2a-
与
的大小,
当3<a<4时,2a-
>
,则[f(t)]min=
;
当a=3时,2a-
=
,则[f(t)]min=
.
∴[f(t)]min=
.
| 2 |
| t |
| 2 |
| x2 |
| 2 |
| t |
| 2 |
| t2 |
即y=-
| 2 |
| t2 |
| 4 |
| t |
| 4 |
| t |
①当
|
| 4 |
| 3 |
| a |
| 2 |
∴f(t)=
| 1 |
| 2 |
| 4 |
| t |
②当
|
| a |
| 2 |
∴f(t)=
| 1 |
| 2 |
| 4 |
| t |
| 4t-2a |
| t2 |
| 4at-a2 |
| t2 |
③当
|
| 4 |
| 3 |
f(t)=
| 1 |
| 2 |
| 4t-3t2 |
| 2 |
| 9 |
| 4 |
综上,f(t)=
|
(2)当1≤t<
| 4 |
| 3 |
| 9 |
| 4 |
| 9 |
| 4 |
| 4 |
| 3 |
| 15 |
| 4 |
当
| a |
| 2 |
| 4at-a2 |
| t2 |
| 2at(a-2t) |
| t4 |
∴f(t)在(
| a |
| 2 |
| a2 |
| 4 |
下面比较2a-
| a2 |
| 4 |
| 15 |
| 4 |
当3<a<4时,2a-
| a2 |
| 4 |
| 15 |
| 4 |
| 15 |
| 4 |
当a=3时,2a-
| a2 |
| 4 |
| 15 |
| 4 |
| 15 |
| 4 |
∴[f(t)]min=
| 15 |
| 4 |
点评:本题是应用题,考查的是导数知识,得到的数学模型是分段函数,考查了分类讨论的思想,研究函数最小值用到配方法、导数法,综合性较强,属于难题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
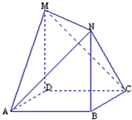 四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1.
四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1. 在平面直角坐标系xOy中,椭圆Γ:
在平面直角坐标系xOy中,椭圆Γ: