题目内容

14．已知{an}是等差数列，Sn为其前n项和，则下列结论一定成立的是（　　）
A．a1a8≤a2a7B．a1a8≥a2a7C．S1S8＜S2S7D．S1S8≥S2S7

分析 对A．B．C．D．利用等差数列的通项公式与求和公式分别作差，即可判断出结论．

解答 解：对于A．a1a8-a2a7=a1（a1+7d）-（a1+d）（a1+6d）=-6d2≤0，∴a1a8≤a2a7，因此正确．
B．由A可知B不一定成立．
C．S1S8-S2S7=${a}_{1}（8{a}_{1}+\frac{8×7}{2}d）$-（2a1+d）$（7{a}_{1}+\frac{7×6}{2}d）$=-$21（d+\frac{{a}_{1}}{2}）^{2}$-$\frac{3}{4}{a}_{1}^{2}$≤0，∴S1S8≤S2S7，故C不一定正确．
D．由C可知D不正确．
故选：A．

点评 本题考查了等差数列的通项公式与求和公式、作差法，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
18．设m，n为实数，则“mn＞0”是“曲线$\frac{x^2}{m}-\frac{y^2}{n}$=1为双曲线”的（　　）
A．充分而不必要条件B．必要而不充分条件
C．充分必要条件D．既不充分也不必要条件
5．函数f（x）的导函数为f′（x），对?x∈R，f′（x）＞f（x）都有成立，若f（1）=e，则不等式f（x）＞ex的解是（　　）
A．x＞ln4B．0＜x＜ln4C．x＞1D．0＜x＜1
2．在等差数列{an}中，a1=1，前5项之和等于15．
（1）求数列{an}的通项公式；
（2）设${b_n}=\frac{1}{{{a_n}{a_{n+1}}}}$，记数列{bn}的前n项和为Tn，求Tn．
9．在直角坐标系xOy，直线l的参数方程是$\left\{{\begin{array}{l}{x=m+tcosα}\\{y=tsinα}\end{array}}\right.$（t为参数）．在以O为极点，x轴正半轴为极轴建立极坐标系中，曲线C：ρ=4sinθ．
（1）当m=-1，α=30°时，判断直线l与曲线C的位置关系；
（2）当m=1时，若直线与曲l线C相交于A，B两点，设P（1，0），且||PA|-|PB||=1，求直线l的倾斜角．
19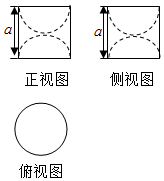．某几何体的三视图如图所示，若该几何体的体积为$\frac{2π}{3}$，则a的值为（　　）
A．1B．2C．2$\sqrt{2}$D．$\root{3}{2}$
6．已知a∈R，直线l：x+ay+a-2=0，圆M：（x-1）2+（y-1）2=1，则“a=0”是“直线l与圆M相切”的（　　）
A．充分不必要条件B．必要不充分条件
C．充分不必要条件D．既不充分也不必要条件
3．已知函数f（x）=x2-2x+1，g（x）=2aln（x-1）（a∈R）．
（1）求函数h（x）=f（x）-g（x）的极值；
（2）当a＞0时，若存在实数k，m使得不等式g（x）≤kx+m≤f（x）恒成立，求实数a的取值范围．
4．已知tanx=2，则$\frac{3sinx+cosx}{cosx-3sinx}$的值为-$\frac{7}{5}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网