题目内容
2.在等差数列{an}中,a1=1,前5项之和等于15.(1)求数列{an}的通项公式;
(2)设${b_n}=\frac{1}{{{a_n}{a_{n+1}}}}$,记数列{bn}的前n项和为Tn,求Tn.
分析 (1)利用求和公式计算a5,再根据通项得出公差,从而得出通项公式;
(2)利用裂项法求和即可.
解答 解:(1)∵{an}是等差数列,前5项之和等于15,
∴$\frac{{a}_{1}+{a}_{5}}{2}×5$=15,
∴a5=5,
∴{an}的公差d=$\frac{{a}_{5}-{a}_{1}}{4}$=1,
∴an=n.
(2)bn=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
∴Tn=1-$\frac{1}{2}+\frac{1}{2}-\frac{1}{3}$+$\frac{1}{3}-\frac{1}{4}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$.
点评 本题考查了等差数列的性质,裂项法数列求和,属于基础题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
13.已知条件p:|x+1|>2,条件q:5x-6>x2,则﹁q是﹁p的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
10.执行如图所示的程序框图,输出的S值为( )


| A. | 4 | B. | 8 | C. | 14 | D. | 18 |
17.已知α,β∈R,则“α>β”是“α-β>sinα-sinβ”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 即不充分也不必要条件 |
7.下列函数中,周期为1的奇函数是( )
| A. | y=cos2πx | B. | y=sinπxcosπx | C. | $y=tan\frac{π}{2}x$ | D. | $y=sin(2πx+\frac{π}{3})$ |
14.已知{an}是等差数列,Sn为其前n项和,则下列结论一定成立的是( )
| A. | a1a8≤a2a7 | B. | a1a8≥a2a7 | C. | S1S8<S2S7 | D. | S1S8≥S2S7 |
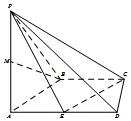 如图,在四棱锥P-ABCD中,AD∥BC,BC⊥CD,点P在底面ABCD上的射影为A,BC=CD=$\frac{1}{2}$AD=1,E为棱AD的中点,M为棱PA的中点.
如图,在四棱锥P-ABCD中,AD∥BC,BC⊥CD,点P在底面ABCD上的射影为A,BC=CD=$\frac{1}{2}$AD=1,E为棱AD的中点,M为棱PA的中点.