题目内容
19．
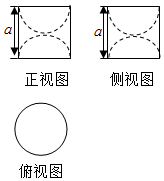某几何体的三视图如图所示，若该几何体的体积为$\frac{2π}{3}$，则a的值为（ ）| A． | 1 | B． | 2 | C． | 2$\sqrt{2}$ | D． | $\root{3}{2}$ |
分析 由三视图可知，该几何体是圆柱中挖去两个半球，用a表示体积，即可求出a．
解答 解：由三视图可知，该几何体是圆柱中挖去两个半球，
∵该几何体的体积为$\frac{2π}{3}$，则$π×（\frac{a}{2}）^{2}×a-\frac{4}{3}×π×（\frac{a}{2}）^{3}=\frac{2}{3}π$，
解得a=2
故选：B
点评 本题考查了由三视图求几何体的体积，属于中档题，
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
10．执行如图所示的程序框图，输出的S值为（ ）
| A． | 4 | B． | 8 | C． | 14 | D． | 18 |
7．下列函数中，周期为1的奇函数是（ ）
| A． | y=cos2πx | B． | y=sinπxcosπx | C． | $y=tan\frac{π}{2}x$ | D． | $y=sin（2πx+\frac{π}{3}）$ |
14．已知{an}是等差数列，Sn为其前n项和，则下列结论一定成立的是（ ）
| A． | a1a8≤a2a7 | B． | a1a8≥a2a7 | C． | S1S8＜S2S7 | D． | S1S8≥S2S7 |
4．已知x∈R，则“|x-3|-|x-1|＜2”是“x＞3”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
8．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左焦点为F，直线y=kx（k＞0）与椭圆C交于A，B两点，若$AF⊥BF，∠FAB∈（0，\frac{π}{12}]$，则C的离心率取值范围为（ ）
| A． | $[\frac{{\sqrt{2}}}{2}，1）$ | B． | $[\frac{{\sqrt{6}}}{3}，1）$ | C． | $[\frac{{\sqrt{3}}}{3}，1）$ | D． | $[\frac{2}{3}，1）$ |