题目内容
6.已知a∈R,直线l:x+ay+a-2=0,圆M:(x-1)2+(y-1)2=1,则“a=0”是“直线l与圆M相切”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
分析 直线l与圆M相切?$\frac{|1+a+a-2|}{\sqrt{1+{a}^{2}}}$=1,化为:3a2-4a=0,解得a即可判断出结论.
解答 解:直线l与圆M相切?$\frac{|1+a+a-2|}{\sqrt{1+{a}^{2}}}$=1,化为:3a2-4a=0,解得a=0或a=$\frac{4}{3}$.
∴“a=0”是“直线l与圆M相切”的充分不必要条件.
故选:A.
点评 本题考查了直线与圆相切的性质、简易逻辑的判定方法、方程的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.不等式x2-x+m>0在R上恒成立的一个必要不充分条件是( )
| A. | m>0 | B. | 0<m<1 | C. | m>$\frac{1}{4}$ | D. | m>1 |
17.已知α,β∈R,则“α>β”是“α-β>sinα-sinβ”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 即不充分也不必要条件 |
14.已知{an}是等差数列,Sn为其前n项和,则下列结论一定成立的是( )
| A. | a1a8≤a2a7 | B. | a1a8≥a2a7 | C. | S1S8<S2S7 | D. | S1S8≥S2S7 |
1.2000年5月,位于咸阳市的陕西省石化建设公司在其院后取土时,发现西汉古墓3座,咸阳市文物考古研究所派人对其进行了清理,发现了较多的文物.其中有一件串饰,如图所示的是一串黑白相间排列的珠子.请问以左边第一颗珠子算起,按照这种规律排列下去,那么第36颗珠子的颜色是( )


| A. | 白色 | B. | 黑色 | C. | 白色的可比性大 | D. | 黑色的可能性大 |
15.已知${log_{\frac{1}{2}}}a<{log_{\frac{1}{2}}}b$,则下列不等式一定成立的是( )
| A. | ${({\frac{1}{4}})^a}<{({\frac{1}{3}})^b}$ | B. | $\frac{1}{a}>\frac{1}{b}$ | C. | ln(a-b)>0 | D. | 3a-b<1 |
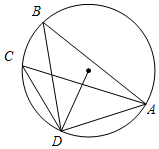 如图,圆内接四边形ABCD中,AD=DC=2BC=2,AB=3.
如图,圆内接四边形ABCD中,AD=DC=2BC=2,AB=3.